Problem Statement:
A group of cities is thinking of adding a waste dump so they can move all the trash away from the residents. They need help figuring out where to place this waste dump. The cities can decide to place their waste dump (assuming the waste dump doesn’t take up any space) anywhere inside the convex hull that encloses the points. They want to place the waste dump in a spot where it minimizes the distance to the closest city (the nearest city lies the farthest).
The above problem can be rephrased as finding the center of the largest circle such that none of the points (cities) lie inside of it. Understanding the solution heavily relies on knowledge of voronoi diagrams. Voronoi diagrams already have another article on this website, but below is a brief overview of them.
If there is a set of points, there are certain sections of the graph where one point is the closest to any point found in that area.

The image is cut up into different sections where there is only one black point in each. The area that each black point is in represents the section of the graph where that black point is the closest point.
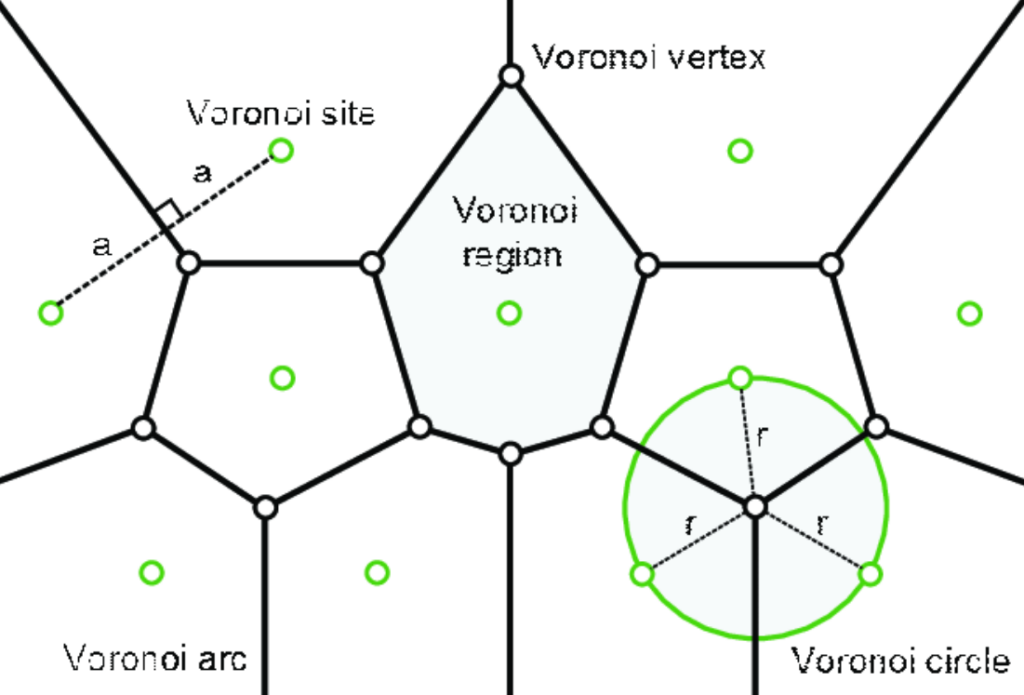
However, there are spots on the graph where multiple points are the closest points. At the edges of each section, there is a spot where two neighboring points are both considered the closest point.
At certain parts of the graph, there may also be voronoid vertices. These are spots where three points can be considered the closest.
It’s impossible for more than three points to be considered the closest.
Algorithm for solving the largest enclosed circle:
The algorithm heavily relies on the understanding that the voronoi vertices (places where three cities can be considered the closest) are the points where the nearest city is the farthest. Placing it at voronoi vertices prevents certain cities from limiting other cities from using their full potential.
If the waste dump is placed inside a voronoid cell, The one point that controls that cell will define the maximum distance. Therefore, preventing the last two points from using their distance to potentially improve the answer
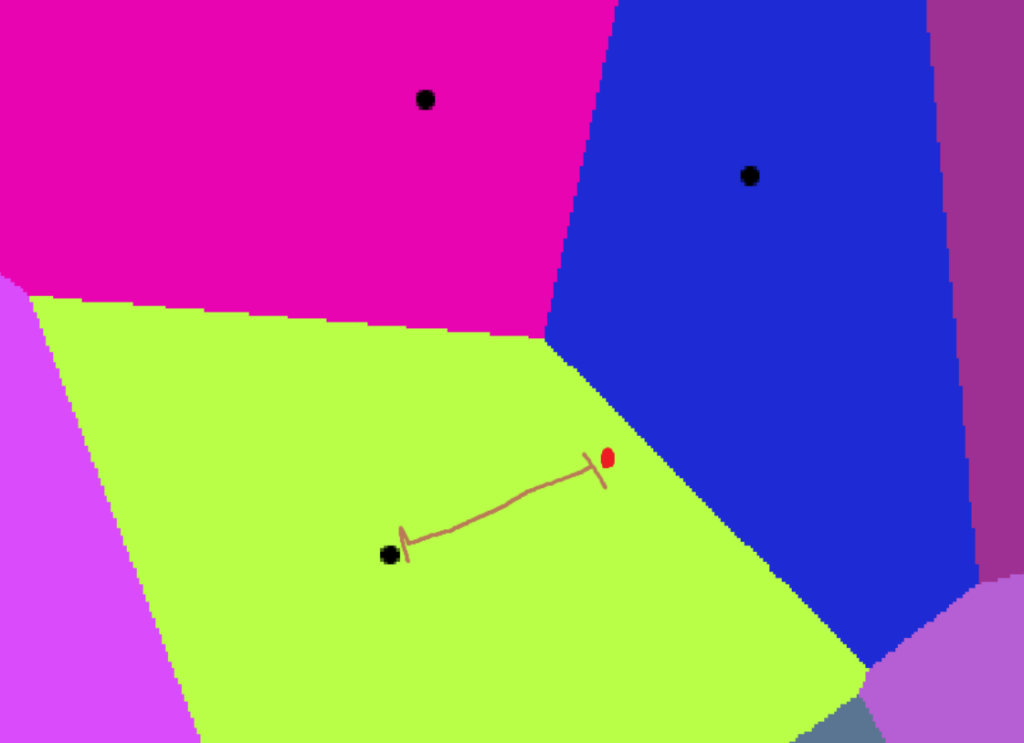
If the waste dump is placed on a voronoid edge, Then, the two points that lie the closest together will define the maximum distance. Therefore, preventing the last point from using its distance to potentially improve the answer
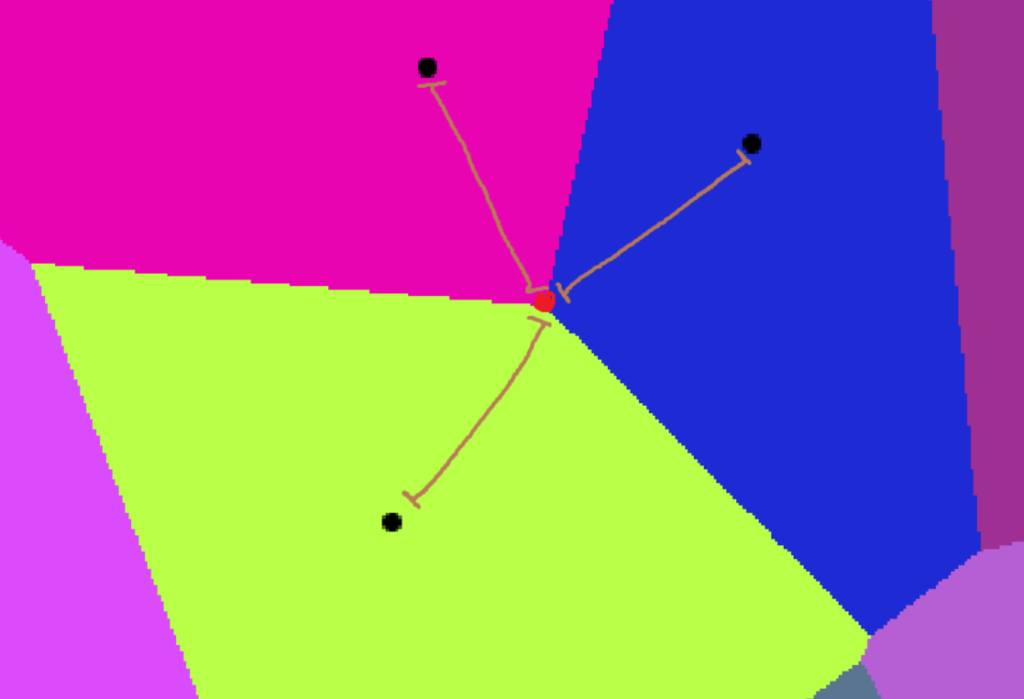
If the point is placed on a voronoid vertex, It utilizes all three points. If you push this point any further in any direction, it will start to decrease the distance to the nearest city.
There are multiple voronoid vertices in each voronoid diagram. So, the algorithm will loop over all voronoi vertices, calculating their distance to the nearest point (city). When calculating the nearest city, it doesn’t matter which city you choose to base that calculation on since, by definition, at a voronoi vertex, the three points that define it are all equidistant from it.
After looping through the voronoi vertices, simply take the voronoi vertex that maximizes its distance from the cities that create it. That voronoi vertex is the center of the circle, and its distance to the closest cities is the radius of that circle.