Linear Diophantine Equations
Linear Diophantine Equations
A linear diophantine equation is described by the following general question: Some linear diophantine equations have infinite solutions, and some have none. It is relatively easy to prove whether the equation even has a solution that abides by the two constraints.
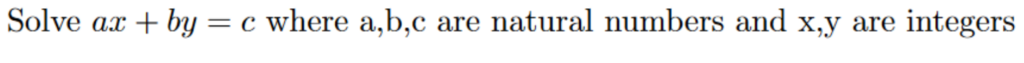
Proving that a solution exists:
Statement: There exists a solution to (ax + by = c) if c is a multiple of the greatest common divisor of a and b.
The proof for the previous statement is shown on the right.
For bigger numbers, calculating the gcd between a and b can be done using the Euclidean algorithm.
If the statement is true, then there are two integers x and y, which can make the natural number C. For finding x and y, the extended Euclidean algorithm can be used.
Proof was inspired by Michael Penn’s video on linear diophantine equations. https://www.youtube.com/watch?v=ZA5FC9ONO3A

Here is a video explaining Linear Diophantine Equations (I did not make this video): https://www.youtube.com/watch?v=ZA5FC9ONO3A
Fermat’s Priminality Test
Fermat’s Priminality Test:
Fermat’s Priminality Test is an algorithm used to determine whether a number is composite or prime. The test is based on the concept explained in Fermat’s Little Theorem:
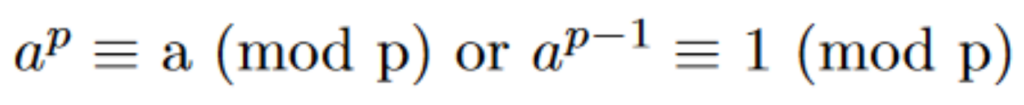
Try testing the theorem. A pattern will appear when composites are used as p and when primes are used as p.
The following video explains why prime p’s will always produce 1’s and why most (discussed later) composites will produce a number that is not a 1.
The following is not my video:
Khan Academy Labs video on Fermat’s Little Theorem: Provides the best explanation and uses a good “non-mathematcal” example to explain the concept:
https://www.youtube.com/watch?v=oUMotDWVLpw
Here are a few examples of testing composite and prime numbers.

Using Fermat’s Little Theorem:
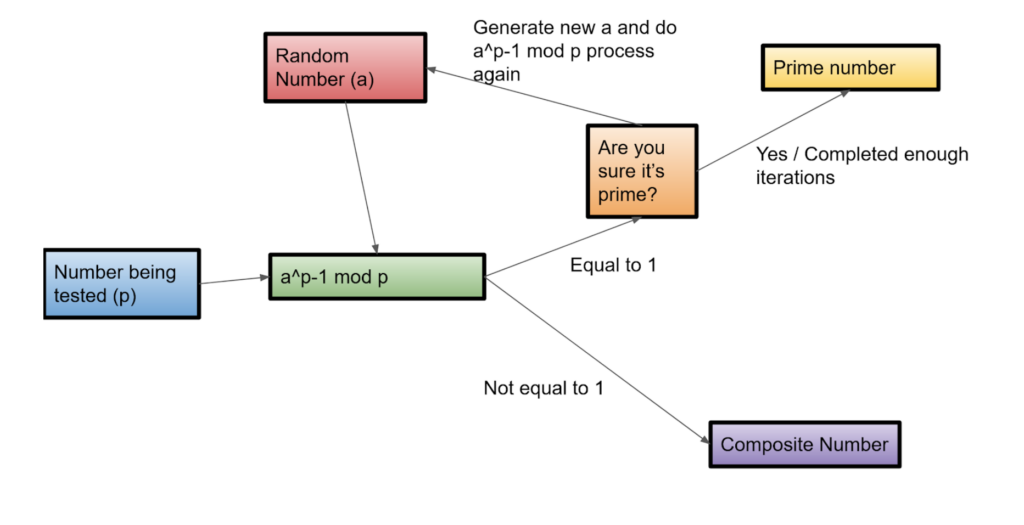
To prove whether a number is prime or not, simply plug it in as p into the equation a^p-1 mod p, where a is a random number. There is a slight issue with this approach. Unfortunately, Fermat’s algorithm has the potential for a lot of false positives. As mentioned, a is a random number. In some cases, a composite number will produce a 1 if matched with a certain a. There is always a chance for false positives, but with enough iterations, the chances of a false positive appearing become impossible. Fermat’s method requires much less calculation than the standard brute-force method for determining primes. The following chart is a good example of how the algorithm will be run: