Introduction:
Diffusion is ubiquitous in the natural world. Diffusion is the gradual movement of something from an area of high concentration to one of low concentration. This can be the diffusion of heat, fluids, chemicals in a solution, etc. An example of diffusion might be putting an ice cube in a drink. When the ice cube is first put in, only its immediate vicinity is cold. As time goes on, the heat will be funneled towards the ice cube. The heat is diffusing and moving from a place of high concentration (high temperature) to a place of low concentration (low temperature). Energy has to be conserved, so the area around the ice cube will heat up and the rest of the drink will cool down. If something is given a long enough time to diffuse, it will reach an equilibrium state where every “part” of the system has an equal concentration, therefore not allowing for any more diffusion. In the ice cube, this would be when the ice cube melts and the drink reaches a uniform temperature. In fact, in the cup example, heat is not the only thing diffusing. The water that comes from the ice will also follow a similar diffusion pattern, spreading to low-concentration areas.
Cellular Automata (using the heat equation):
For the sake of explaining how diffusion occurs, it’s best to explain how it is approximated. Let’s assume that we are currently working with heat diffusion. In order to simplify the problem, we are going to represent it using a grid. Each tile in the grid will have its own temperature and will interact with its neighbors. The process will go through iterations where every single tile will be updated simultaneously.
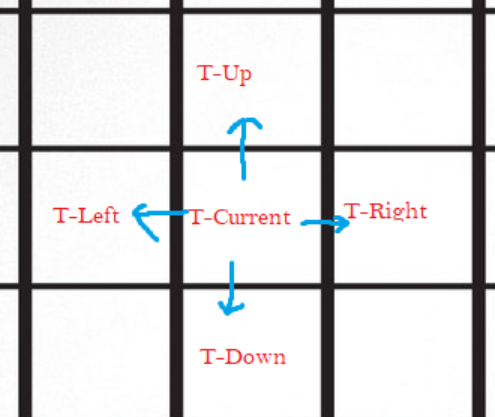
We are going to consider each tile and its immediate neighbors (up, down, left, and right) separately. For each tile, it wishes to reach equilibrium with its neighbors. Each of its neighbors will either have a higher or lower concentration of the tile in question. If one of the neighbors has a lower concentration, the center tile will diffuse into it, and if a neighboring tile has a higher concentration, it will diffuse into the center tile. The total change in temperature the center tile experiences will be equal to the following:
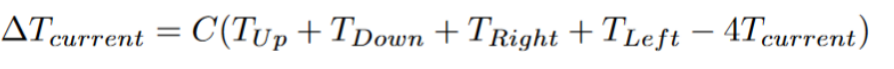
We simply sum over the difference between the neighbors and the center tile. In order to fine-tune the equation, we also attach a constant to control the rate. The equation also sheds light on how the rate of diffusion changes in relation to concentration. If a neighboring tile has a massive concentration difference (significantly more concentrated or significantly less concentrated) relative to the middle tile, it will have a profound effect on the state of the central tile in the next iteration. While neighboring tiles with very similar concentrations to the middle tile will have very little effect. If you let diffusion take its course without intervention, then the CHANGE in concentration in each tile will continue to decrease. The process of diffusion will start fast and become slow (the idea of rapidly decreasing as the difference decreases can be seen in Newton’s Law of Cooling).
While iterating through every tile and checking neighbors, you might realize that not every tile has the same number of neighbors. That issue calls for certain boundary conditions. At Least for heat diffusion, most simulations choose to simply remove the values from consideration when calculating the next state. For edge (3 neighbors) and corner (2 neighbors) pieces, the calculator for the next state might look like the following:
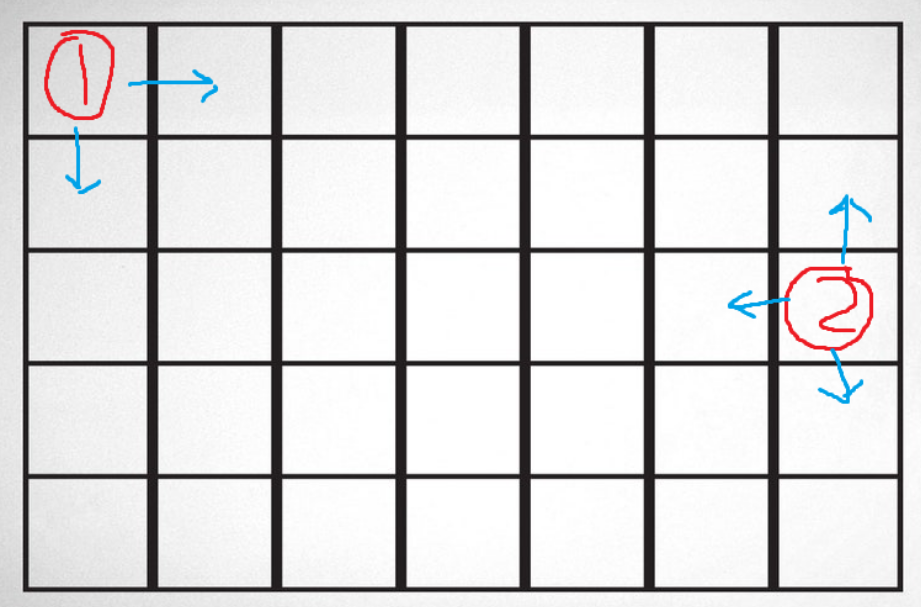
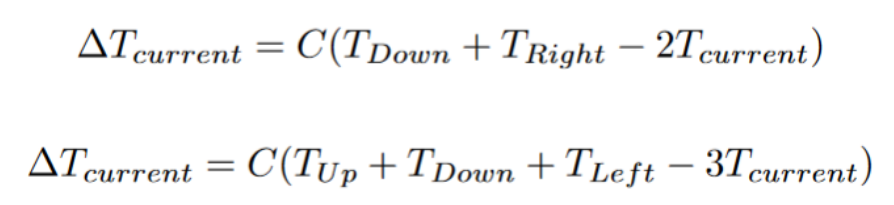
1st Equation = Top Left Corner Tile
2nd Equation = Right Boundary Tile (not a Corner)
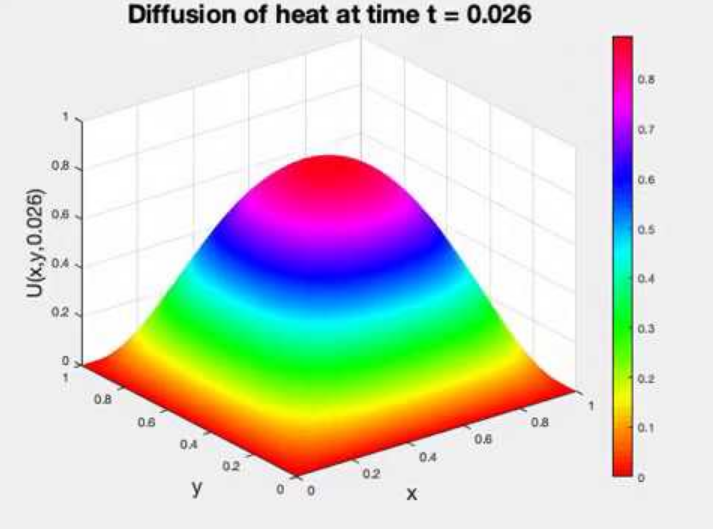
Eventually, areas of high temperatures will spread out to areas of low temperatures. After enough time, the entire grid will share the same temperature. Refer to the below animation, which starts with an area with high potential in the middle.
Here is an animation of the diffusion effect (I do not own the video): Video Link
For those interested in the simulation
A note for people who are actually interested in the algorithm for simulating: we do not update the temperature as we check each tile in the grid. We need to save the changes and apply them all at the same time. The process usually requires a large system of equations. The below video uses fluid diffusion instead of heat diffusion, but the process remains the same.
Some Mathematical Approaches:
I question my ability to talk about diffusion from a mathematical standpoint, but here it is anyway. In the above example, we used an approximation of diffusion by discretizing the actual real equation. The real 2-dimensional heat equation is the following:
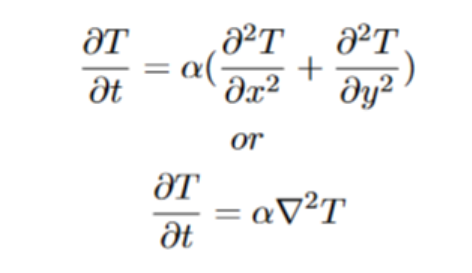
I’m not going to explain how to use discretization for approximation, but this video does a very good job at it. (I do not own the video) Video Link
All of the diffusion equations have a common mathematical symbol called the laplacian. The laplacian is an operator that acts on a scalar function. Taking the laplacian of a function is equivalent to finding the divergence of the gradient of that function. It is also equivalent to the sum of all second-order partials with respect to each independent variable. Remember that the second partial is the rate of change of some function.
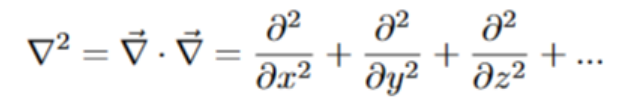
For the heat equation, the rate at which temperature at a certain point is changing will increase if “neighboring” points are also quickly changing. If certain points aren’t changing much, then any diffusion equation predicts that the points around them aren’t changing that much as well.
The laplacian operator can be seen directly in the Navier-Stokes equation, which describes all newtonian fluids. In the case of Newtonian fluids, they will have diffuse momentum. It can also be seen in Laplace’s own equation, which describes how electrical potential will move around in a system.
More Generalized Diffusion for Particles:
Fick’s Law of Diffusion describes the rate of particle movement within a container. Let’s say you have a box and on side A of the box you have a high concentration of some type of particle and on side B (the opposite side) you have a low concentration. Fick’s Law describes the rate at which particles diffuse from side A to side B. There are many different factors that might impact how fast the particle diffuses.
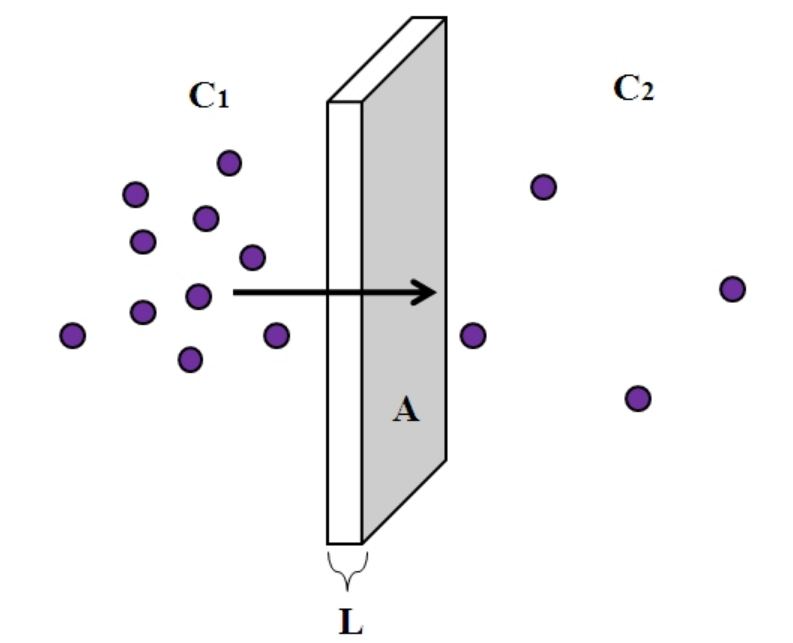
#1: Decreasing the Distance Between Sides A and B
Obviously, if you make the distance between side A and side B smaller, the rate at which the particles travel between each side is faster since there is just less room to cover.
#2: Increasing the pressure difference
We also know that particles like to travel from areas of high concentration or pressure to areas of low concentration or pressure. So, if we increase the pressure difference between the two sides, it would expedite the rate at which particles travel. That can be done by either adding more particles or taking particles away.
#3: Decreasing the molecular weight
We also know from Graham’s Law that the speed of a particle is inversely related to the square of its molecular weight. Assuming the temperature in the system stays the same, a smaller particle will, on average, move faster than a large particle. It does this in order to maintain constant kinetic energy.
#4: Increasing the surface area of side B
Increasing the size of side B would also increase the rate at which particles diffuse. Since there is more room for the particles to move around,
All four factors can be seen inside Fick’s equation of Diffusion which is the following:
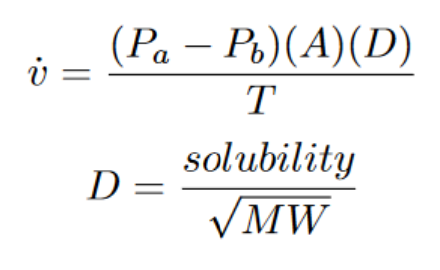
D = the diffusion constant (decreasing the molecular weight).
T = Distance between sides A and B = Thickness (decreasing the distance between sides A and B)
Pa-PPb = difference in pressure between side A and side B (increasing the pressure difference)
A = cross-sectional area of the box (increasing the surface area of side B)
You might also see Fick’s Law written in the following form:
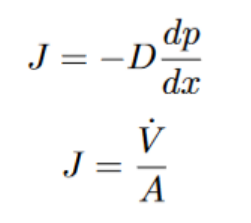
J = the flux, which is the rate of particles passing through a specific area.
dp/dx is the gradient and the change in pressure over a certain distance.