Lagrangian Mechanics – eggshellwarriors

Introduction

The best place to start learning lagrangian mechanics is with a familiar (hopefully) example from classic Newtonian physics: calculate the average velocity of a ball in free fall. Most people would look towards using the conservation of energy laws to solve this problem. Before it is dropped, all the energy in the ball is stored as gravitational potential energy. When the ball is dropped, it converts that potential energy into kinetic energy, and right before it hits the ground, the ball is all kinetic energy. So, its logical sound is potential energy = kinetic energy. Solving the equation for velocity will give you the following:

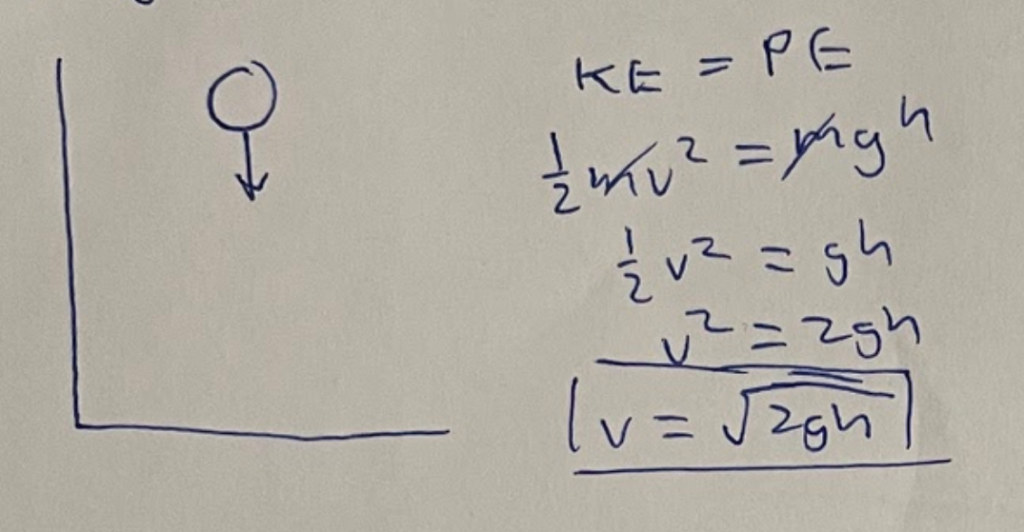
This example is great for the conservation of energy because all potential energy was converted into kinetic energy. Although this method might appear limited in its applications, it can be applied to every single scenario.

The Lagrangian is based on the idea of action, which is the difference between kinetic energy and potential energy (L = KE minus PE). The idea of action is further established by the action functional, which is a line integral of the lagrangian over some path. Let’s go back to the free-fall problem. For the moment, let’s unbind ourselves from reality and ask how many different ways there are for the ball to go from the top to the bottom. There are infinite ways it can fall straight down, it can curve, etc. Each path (curve) will have different properties. If you used the action functional integral, summing the lagrangian at each point on the curve, you would find varying amounts of “action”. The cornerstone of lagrangian mechanics is the principle of least action, which states that the path that takes the least action is the path the object actually takes.

The path with the least action is the line that falls straight down. It is the most efficient way to get from the top to the bottom. Any curves in the path would lead to a higher total action. The object takes the easiest path. You might have heard that electrons take the path of least resistance; this is the same principle.

In order to capitalize on this discovery, Lagrange (and Euler) formed the Euler-Lagrange differential equation, which is used to minimize action (therefore finding the equation of motions). In calculus 1, many students are exposed to optimization problems such as finding the minimum value of xy such that x+y = 60 (by the way, x = 1 and y = 59). In those problems, you are finding an optimized scalar value like the number 59. In the Euler-Lagrange equation, you are finding an optimized function that, in this case, minimizes action (this is called the calculus of variation). The equation goes as follows:

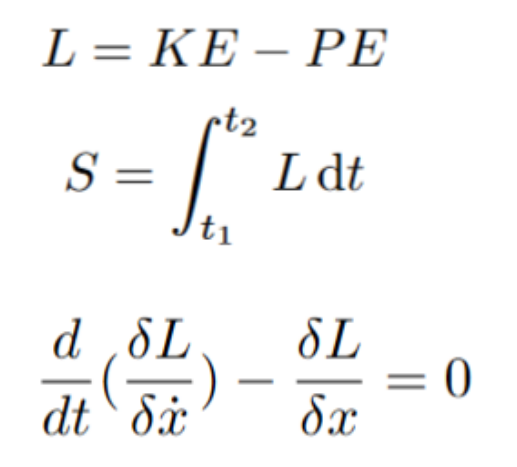
Honestly, I don’t remember how it’s derived, but I’m sure it’s out there somewhere. It is kind of hard to explain how the equation works, and it’s probably best to return to the free fall problem for one final time as an example of its uses.

As mentioned prior, the lagrangian is defined as the difference between kinetic energy and potential energy. It will yield the following:

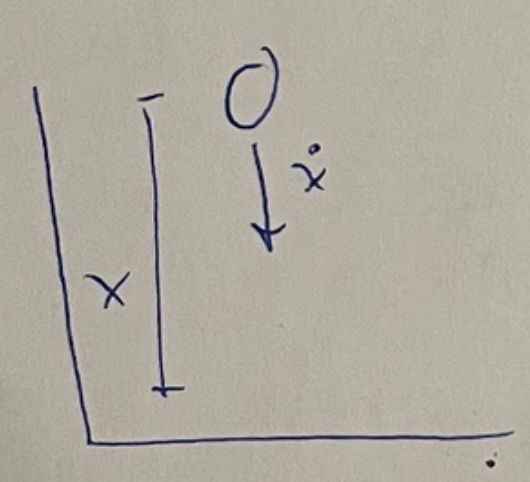
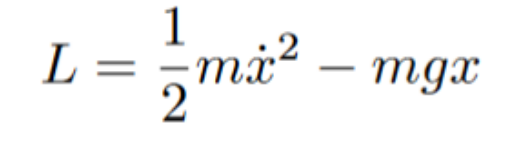
Assume that x is our spatial variable. This makes the x dot (the derivative of x) the velocity. Taking the partial derivative of the lagrangian with respect to velocity and position will give the following:

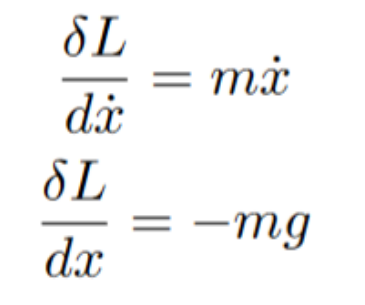
Now, after plugging these into the Euler-Lagrange equation, we still have to settle the time derivative part. Since velocity is a function of time, it will become the 2nd derivative of the position coordinate (better known as acceleration).

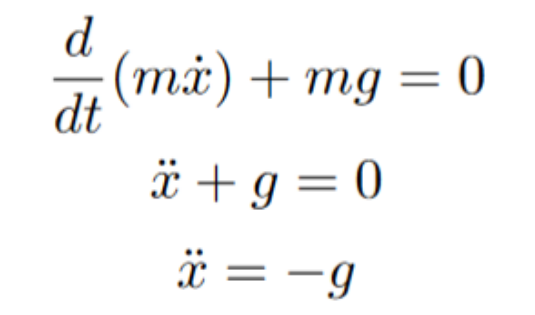
After factoring out and removing mass, we are left with our equation of motion. If we move the g around to the other side, we will hopefully get a familiar result. The acceleration of the system is equal to gravitational acceleration. However, we can take this a step further by finding the actual position of the ball instead of just its acceleration. Integrating once with respect to time will give us the following (remember, our “constant of integration” is not a constant but a function of x single dot):

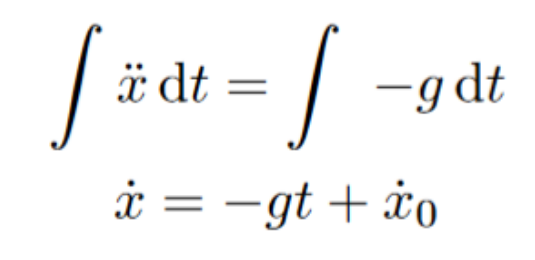
Integrating both sides again with respect to time, we get the following:

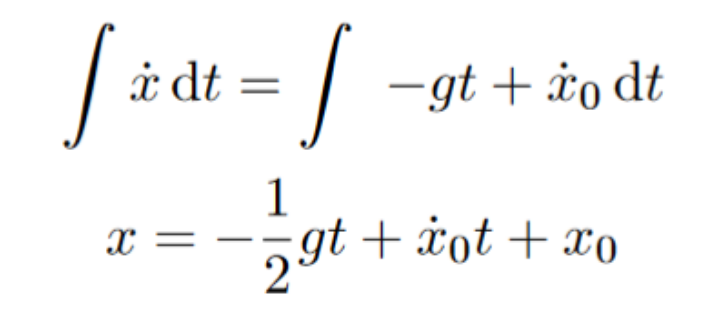
Again, we get a very familiar equation. This is the same kinematic equation that is drilled into every single physics student’s mind. X dot represents an initial velocity, and c represents an initial position. You may not be convinced of the power of lagrangian mechanics yet, so here are even more examples.

Spring System:

The process for solving the equations of motion in a spring system is very similar. The primary difference is that the system has elastic potential energy rather than gravitational potential energy.

At the end of the process, you are left with a second-order homogeneous differential equation, which, when solved, gives the following (also note that angular velocity is equal to the square root of k/m):

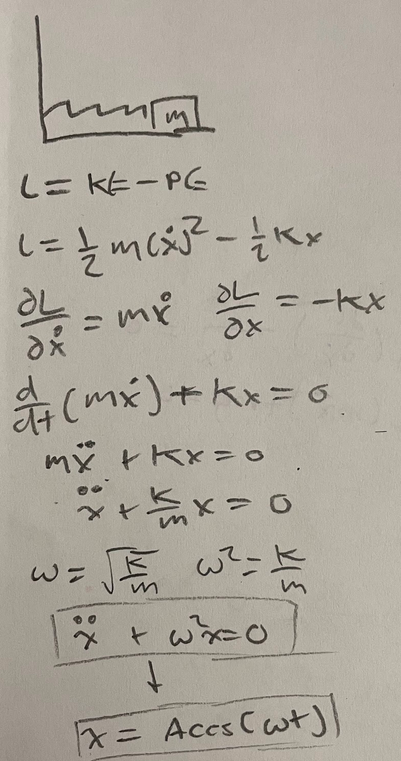
Pendulum:

This one is a little different. Representing kinetic energy in terms of velocity might not be ideal for modeling the system. The pendulum system is better represented using an angle: theta. Conveniently, there is a way to represent kinetic energy in terms of angular velocity. Due to the nature of the pendulum, the potential energy is also a function of theta. However, with the use of a little bit of trigonometry, this issue can be resolved, and the solving process becomes very similar to the two previous problems.

More about Lagrangian mechanics:

I’m too lazy to explain more about lagrangian mechanics (nor am I credible when it comes to more advanced applications). It’s also important to mention that the formula is not limited to positions and velocity. The lagrangian can be used to minimize anything as long as you have an optimizable function. Here is a list of other things that can be done with the lagrangian mechanics that stood out:

Equation of motion for coulombic forces and gravity (multivariable lagrangian mechanics):

Disclaimer: We assume that one object is static and the other is moving and being attracted to it.

Coulombic forces (assume only attractive coulombic forces) and gravity both apply attractive forces that are proportional to the inverse of the distance between the two interacting objects. These forces are what cause the movement of electrons and the orbiting of planets. It’s kind of lame to tackle this problem in 1D (only x and x dot), since stuff like gravity between big objects is synonymous with circles or ellipses, which exist in 2D.

There are two scales to do the problem under. You can stay in rectangular coordinates and let your position and velocity be in terms of the two variables x and y. Alternatively, you can move to polar coordinates and use r and theta.

Since there are two variables (x/y or r/theta), you will end up with a coupled differential equation that is your equation of motion.

I couldn’t find a proper link for a resource that has the solution.

Catenary:

If you hang rope across a gap, what shape will it form when under its own weight? What shape minimizes the stress the rope is under?

Image Source

Below is a video detailing the caternary problem (I do not own the following video): Video Link

Brachistochrone:

Assuming a uniform gravitational field, what is the fastest way from point A to point B (assuming point A is above point B)? By the way, the answer is not a straight line.

Image Source

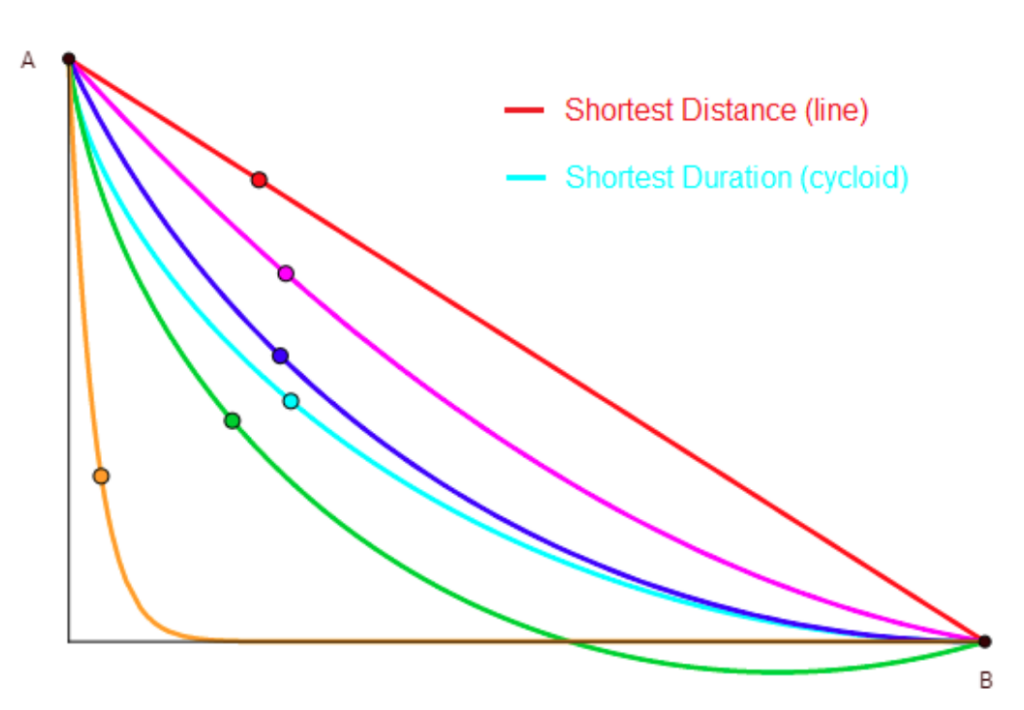
Here is a video detailing the Brachistochrone problem (I do not own the video): https://www.youtube.com/watch?v=zYOAUG8PxyM

Snell’s Law (Fermat’s Principle):

Nothing is excused from Lagrangian mechanics, not even light. It turns out that light too wants to travel the path of least resistance and thus travels in straight lines.

Image Source

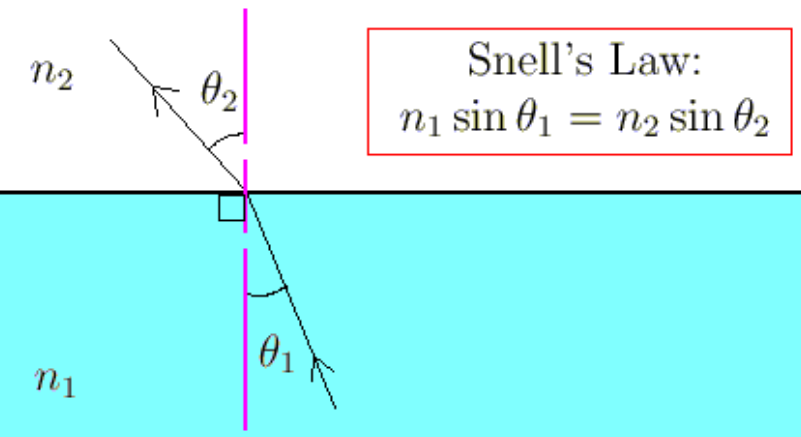
Here is a video detailing Snell’s Law problem (I do not own the video): Video Link

Geodesics:

Since we live on the surface of a sphere, using pythagoras to figure out the distance between two places is only accurate at short distances. It assumes that we can travel through the Earth. The curve of the earth makes paths longer. A geodesic is the shortest path between two points on a surface where the path stays on the surface.