3D Convex Hulls
2D convex hulls provide some basis for the building of 3D convex hulls. 3D convex hulls provide the basis for building N-dimensional convex hulls. The 3D convex hull has the exact same behavior as a 2D convex hull, but this time there can be three different variables being accounted for. However, building them is a little harder than two-dimensional.
Visiability
Figuring out which points see a certain face and which points do not see a certain face is important to the construction of a 3D convex hull. Imagine a plane coming from the face that is currently being considered. One side of the face points towards the outside, and the other face points towards the interior of the convex hull. If a point X is on the exterior side of the plane, it is to be considered to be visible. If the point is on the opposite side, then the face is not visible from that node.
In the following image, the current face is visible at point B but not at point A.
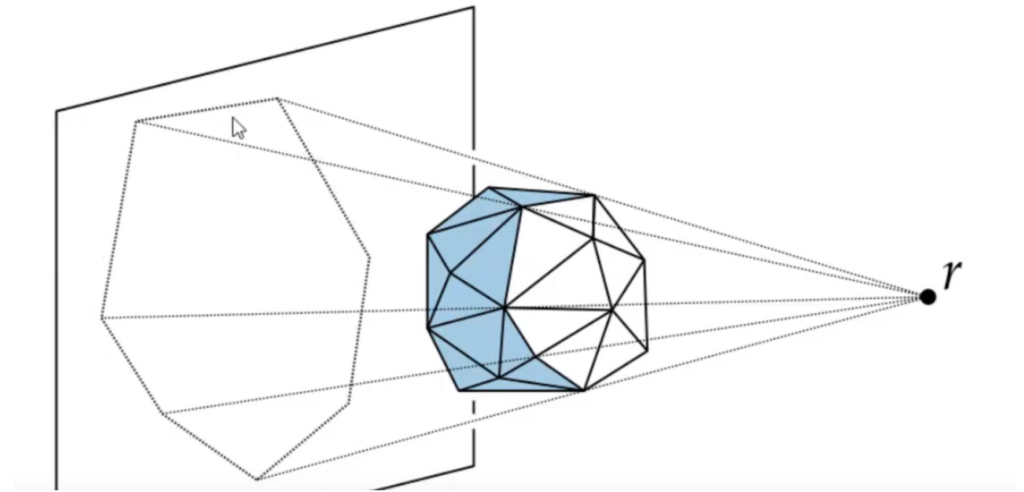
Throughout the process of constructing the convex hull, what faces a point can see will be queried and asked often. So, this information will be stored in a conflict graph, which is a bipartite graph with points on one side and faces on the other. The conflict graph will contain all of the nodes that have not been processed. Then, there exists an edge between a point and a face if the point can see the face.
Constructing a 3D convex hull using the Randomized Incremental Algorithm:
Firstly, a convex hull is needed before starting to build with more points. This has to be done by brute force by building a convex hull from four different points that are not co-planar. This will form a tetrahedron. The rest of the points that were not used in the initial convex hull will be shuffled and have a randomized order, improving the average running time. It is best to construct the conflict graph now using only the points that are part of the initial convex hull. After that, the points will be traversed in their random order. There are two major scenarios for dealing with the points.
The point already exists inside the convex hull.
To determine whether a point exists inside the currently established conex hull, the conflict graph should be consulted. If the current point has zero connections in the conflict graphs, it can see zero faces. So, it already exists inside.
The point is on the outside of the convex hull.
This starts by removing the faces with which the current node has conflicts. Do not delete it from the conflict graph, but the information that supplies the information to the faces of the graph. As the face will no longer be visible after this current node has been processed, it is still needed while computing the new shape.
Now find all of the horizon edges. This can be done by going through all of the edges of the faces that are connected to the current point via the conflict graph. Make sure that the edges that are counted are the boundaries of the entire visible shape, not the boundaries of each individual face. This can be done using the information that a convex polygon does not have any concavities.
The following image is not mine. It is from the following video: https://www.youtube.com/watch?v=ylqqa-TiDvg&list=PLubYOWSl9mIvTio-1bXWnhE9LdeXfox1z&index=41
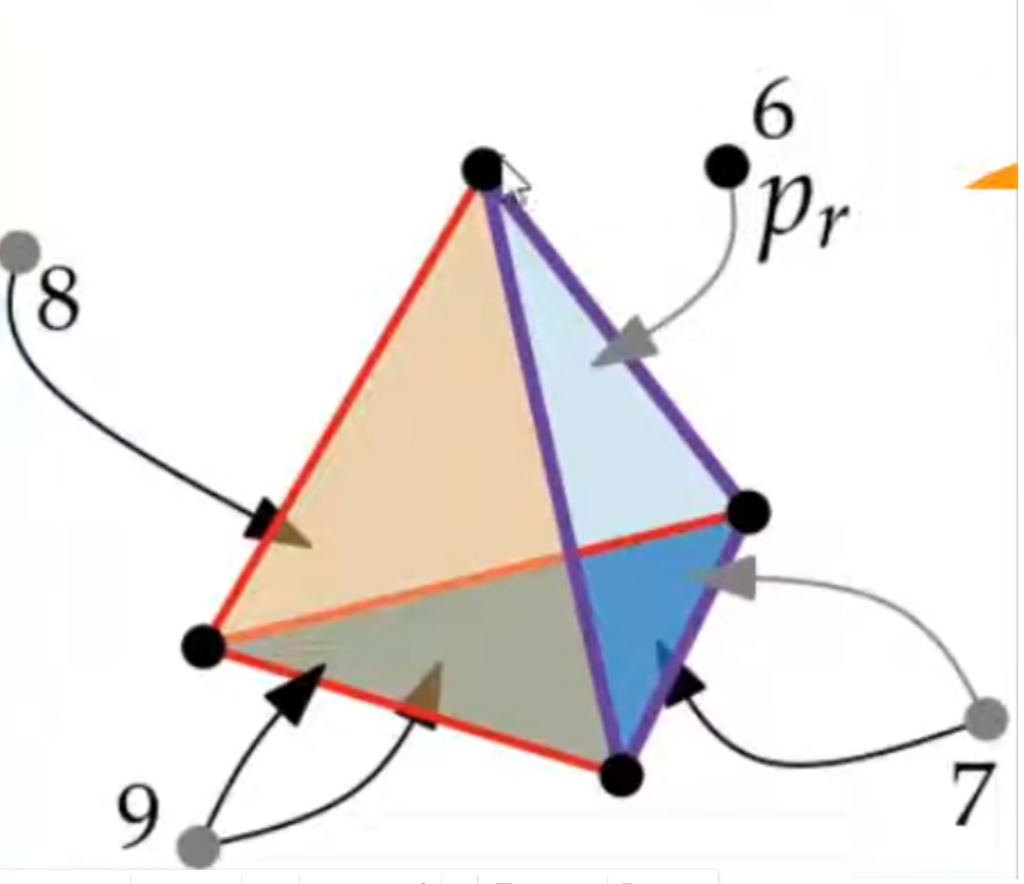
For every edge on the horizon, a new triangle face needs to be constructed between that edge and the new point being added. Unfortunately, now that the new face has been added, the conflict graph needs to be updated. We do not necessarily need to check every point to see if it sees the new face. The new face is a triangle, and it is made up of 1 original edge and 2 new edges. The original edge was a shared edge between multiple different faces. One of these faces will always be the one that was deleted earlier. Only the points that see any of the faces that the edge was a part of need to be checked (including the ones that see the now deleted face). After the entire horizon has been considered, can the old face finally be deleted from the conflict graph?
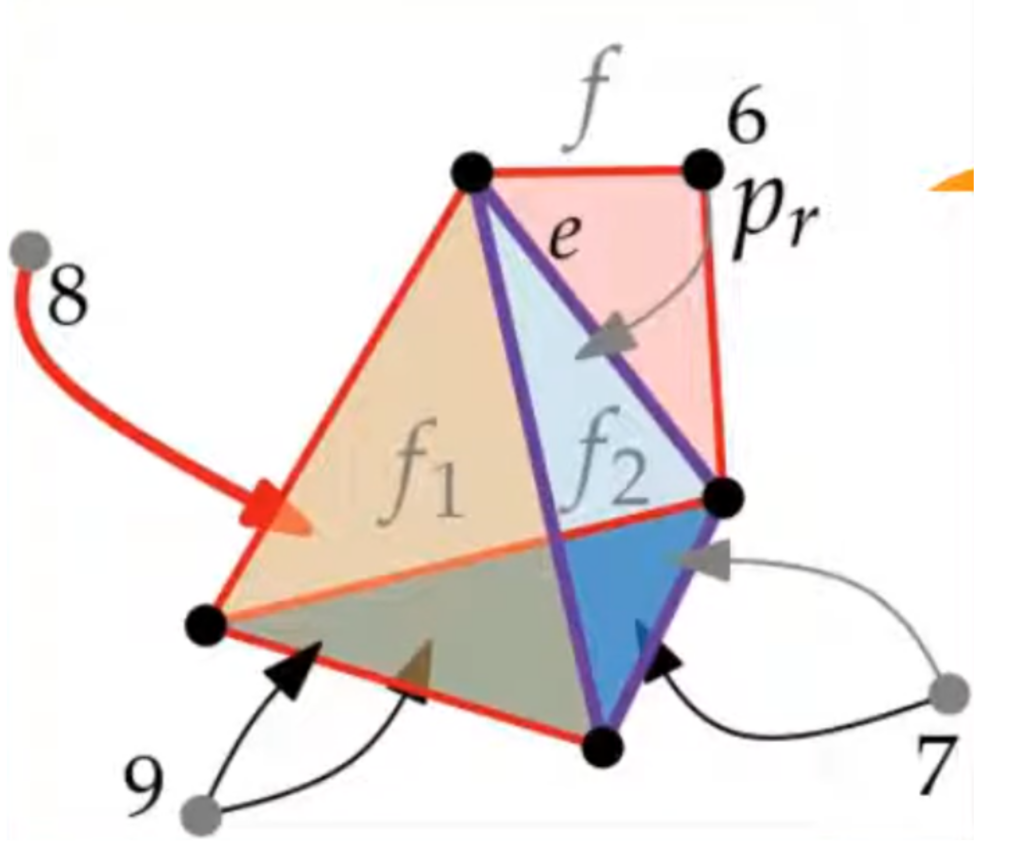
In the following image, point 6 is being added. The current edge e is being used to create a triangle with point 6. To figure out which different points can see the new face that e and point 6 are making, the faces that are apparent are potential candidates. The edge e was connected to the edge that got deleted (f2) and the edge in the back (f1). Only the points that show any of those faces need to be checked. For example, in this case, point 9 doesn’t see either of the faces, so there is no need to consider it.
The following image is not mine. It is from the following video: https://www.youtube.com/watch?v=ylqqa-TiDvg&list=PLubYOWSl9mIvTio-1bXWnhE9LdeXfox1z&index=41
Runtime:
Calculating the runtime for the 3D convex hull construction is weird. If you revist the the instruction it might seem that the algorithim will run in cubic time. But, it can be proven that a convex hull in 3 space can be made in only O(n log n).
I do not own the following video. The video provides an analysis of the time complexity of the 3D convex Hull https://www.youtube.com/watch?v=0bJK2qIouD4&list=PLubYOWSl9mIvTio-1bXWnhE9LdeXfox1z&index=43