Determining whether a point lies inside a polygon is a common question in the field of computational geometry. Figuring out whether a point lies inside a polygon can be done in linear time if the shape is concave and logarithmic time if the shape is convex.
For concave and convex shapes (ray casting method)
Initially, the idea of deciding whether a point lies in a polygon might feel a little complex. The concept of figuring out what side is inside the shape is what confuses me most. However, whether a point lies inside a polygon can be reduced to an odd or even intersection relationship.
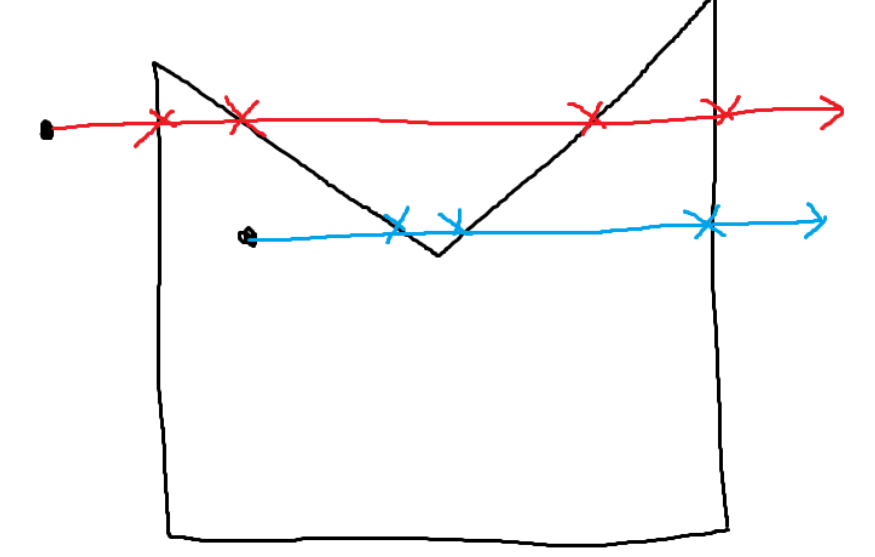
Let’s say you have a point and a triangle. If you draw a ray in the direction of the triangle from the point, observe how many intersections there are when the point is on the inside and when the point is on the outside.

When the point is outside the triangle, we can see that the ray intersects the polygon twice. If the point lies inside, then the ray only intersects the polygon twice. These observations lead to the following statement:
A point lies on the inside of the polygon only if you can draw a ray in any direction from the point, and it will intersect the polygon an odd number of times. (There are a few caveats to this statement; this will be discussed at the end.)
With a little bit of thought, the base case example can be scaled up to any type of polygon. Since if you enter a section of the polygon, you must exit at two intersections, But if you’re already inside the polygon, the intersection where you first entered is gone.
This algorithm works in O (n). You would simply take the ray produced from your point, compare it to every line segment, and see if it intersected.
For convex shapes
Convex shapes bring a lot of key properties along with them. One of those is the ability to determine whether a point lies inside the polygon in O(log n) time.
It starts by taking the convex shape and splitting it into an upper hull and a lower hull. There are videos online about how to do this. Regardless, we just want to end with a shape that is split up into two parts stacked on top of each other. c
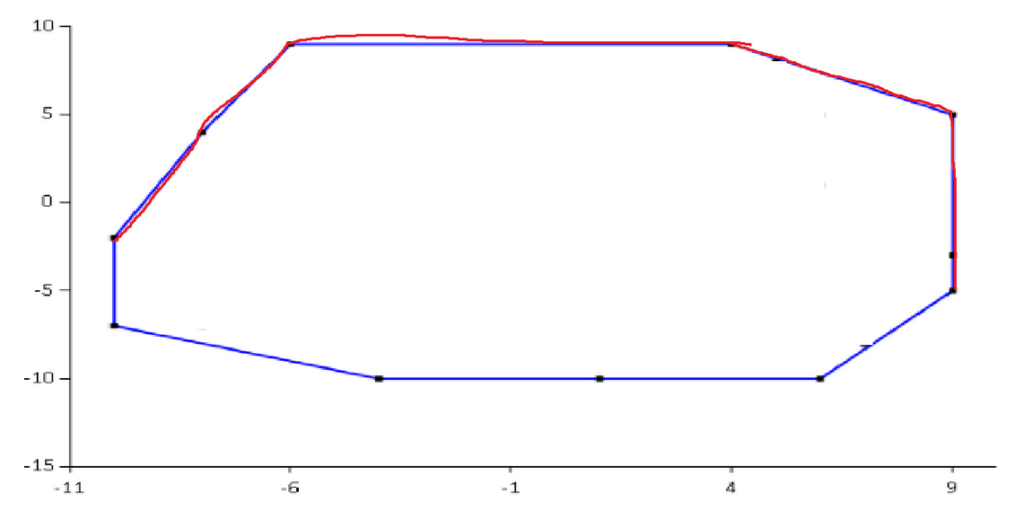
The algorithm first decides if the point is under the top hull and then decides if the point is above the bottom hull. If both of these are true then, the point lies inside the convex polygon.
In most cases the top hull and bottom hull are all sorted from left to right according to their x coordinate. If you have a point this means you can binary search the section of the hull that lies above or below.
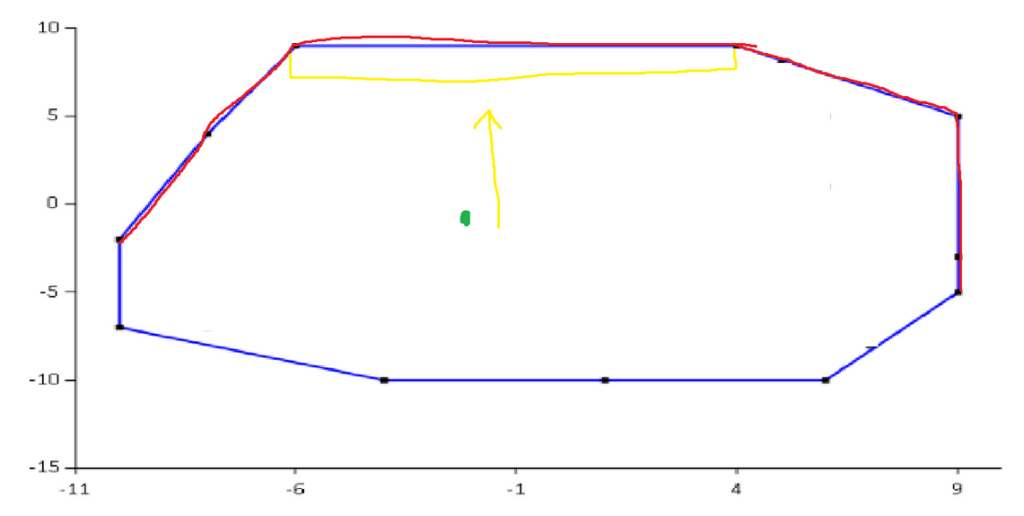
If you test the green point through binary searching the top hull you figure out that the yellow interval is the corresponding section. Since, the green part lies below the section it found for the top hull it still has potential to be considered inside
Now do the same for the bottom hull.
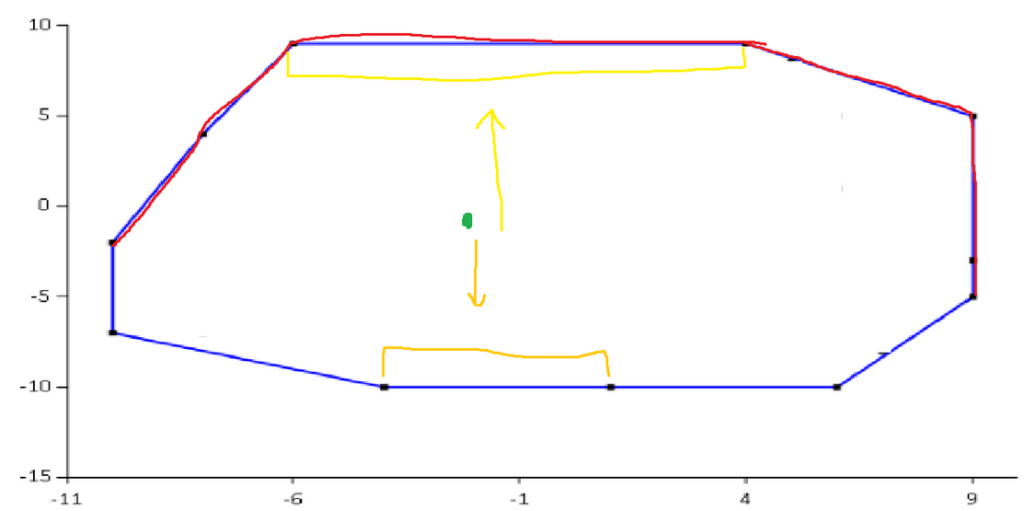
The corresponding interval for the green point in the lower hull is the light orange interval. The green point lies above this interval, so the point lies inside the shape.
You may not have noticed it, but we tested whether the point was valid on the x-axis and y-axis in this process. Had the point not found a valid interval for either the top hull or the bottom hull, we would have known that the point didn’t lie in the shape.