What is Diffie Hellman?
Diffie Hellman is a cryptographic key-exchanging method. It was used to get messages across the internet while only allowing the two people involved in the conversation to see the messages that had been sent. There are two main ways to differentiate Hellman. One involves modular arithmetic, and the other uses elliptic curves.
Colors Example:
Let’s say that John and Bob wish to talk to each other over the internet. John has his own private section, and Bob has his own private section that nobody can see. In order to communicate, they must send the information over the internet, which is open for attackers to see. Each person in a different Hellman exchange has a private key that they share with no one. For their connection, there is also a generator (g) value and a large prime number (p) value. For this current example, assume that generate and prime are grouped together. Their uses will be explained later.
Refer to this slideshow that I made which exands ont he color analogy through an example.
https://docs.google.com/presentation/d/1R3W1Vdxy9VUzUMwP0Fk9JanEfBVGG2CtX47ZwIvhP74/edit?usp=sharing
In the end, both John and Bob have the same final key (the color brown). Due to the nature of colors and how differently Hellman operates, it doesn’t matter the order in which the colors were applied. Red mixed with yellow is the same as yellow mixed with red. What mixing means in Diffie Hellman will be explained later. But, as of right now, assume it is impossible to reverse engineer it. This means that a certain value cannot have specific components taken out of it. The value g cannot be derived from the value bg. If you look back at the demo, you can see that there isn’t a way to derive the message just from the information in the public space.
Modular Diffie Hellman:
Modular differential equation Hellman uses the idea of modular arithmetic. Modular arithmetic can be thought of as doing math around a clock. When a value is modulo’d, the remainder from division is returned. So 16 mod 3 is 1 because the remainder of 16 divided by 3 is 1. You can think of it as a cycle or a clock.
If there is b mod n, The value b will loop back around once it reaches n instead of continuing. Modular arithmetic is a weird subject, and it is recommended that more resources be used. Refer to the following example, which is identical to the one above but this time with real values.
But why is modulo used to differentiate Hellman and so many other crytographic techniques? When a value is moduloed, it’s extremely hard to come up with the original values used, as there’s no telling how many times it went through the cycle. Examples given:
If the output of B mod 2 is 1, then what is B? B could be any of the following values:
1 because 1 mod 2 is 1.
3 because 3 mod 2 is 1.
5 because 5 mod 2 is 1.
(2n + 1) because (2n + 1) mod 2 is 1.
There are an infinite number of possibilities for the starting value, making it nearly impossible for an attack to derive any of the values directly from the equation.
If this wasn’t very clear, refer to the second video in the sources.
Ellipitical Curve Diffie Hellman
There’s another way to use differential equations using elliptic curves and tangent lines. The equation of an elliptic curve is y^2 = x^3 + ax + b. Where a and b are different parameters that can be changed to alter the shape of the curve. In the previous example, the point was cycling around a clock. In this technique, our point is bouncing around an elliptic curve.
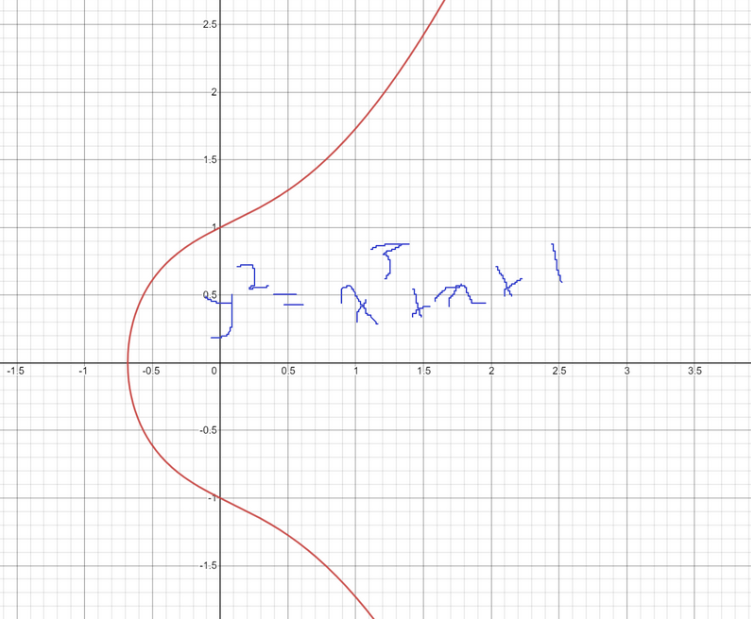
Very similar to the modular differential equation, we start with a generator value (call that g). Instead of just a single number, it will be an ordered pair that lies on the elliptic curve. For the very first iteration to find the next point, the algorithm will run:
Find the horizontal line that intersects g. Then, find where that line intersects the elliptical curve. Place the next point there, then reflect it across the x axis.
For every other iteration:
Find the line between the initial generator value g and the last point that was calculated. Then, find the point at which this line intersects the elliptical curve that is not at the first two points already mentioned. Take that point and then reflect it along the x-axis.
The following methods will not work on all elliptic curves. More about this later. Refer to the following demo for a better understanding of how new points are found.
Finding the initial generator value of an elliptic curve tends to be harder than finding the initial generator value of a modulo. This means that elliptic curves can use shorter key lengths, saving a little bit of time. Elliptical curves are used to simulate randomness and to make it appear like the point is jumping around with no pattern. However, this effectivity completely depends on the parameters of the curve. One of the most popular curves actually had a possible backdoor.
If you are interested, refer to this video. I do not own it, and it is sourced at the bottom. https://www.youtube.com/watch?v=nybVFJVXbww