What is a dominator tree?
A dominator is a tree where the nodes in the tree are ordered by dominance. Each node’s ancestor is dominant over it. This means the root of the tree dominates all nodes. For u to dominante v. Then every path from the root to v must pass through u. Think of it as a bottleneck node.
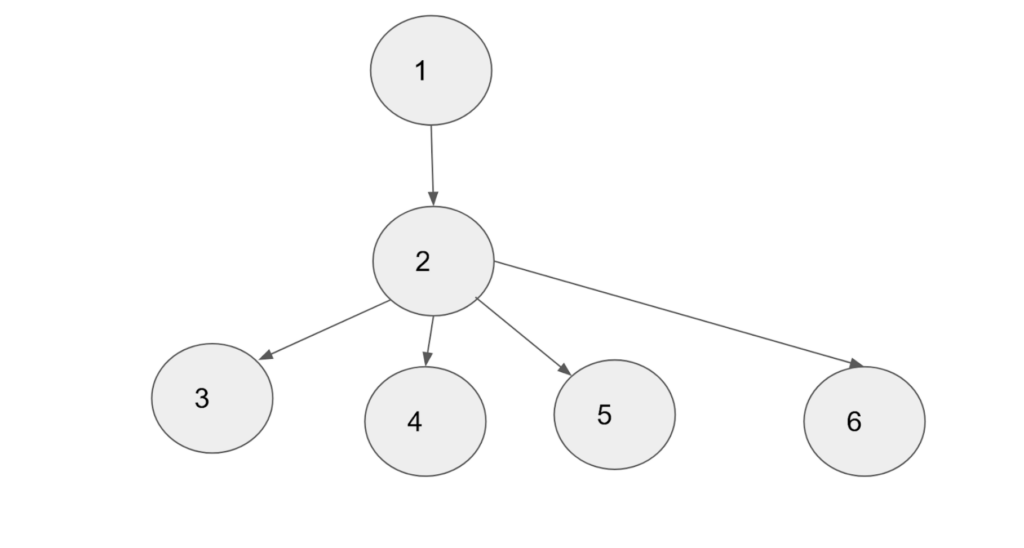
The previous graph will produce a dominator tree like below. In this case 1 dominates 2 and 2 dominates the rest of the nodes. If a node in the dominator tree was to be removed then, it would create to disjoint groups. Nodes 3,4,5,6 all rely on 2 to be conneceted to the rest according to the graph. If node 6 was to disappear in the graph then, it wouldn’t create disjoint groups since from the dominator tree it is connected/dominating nothing.
Couple of properties
Dominance has transitivity. For example, if u dominates v and v dominates w, then u also dominates w.
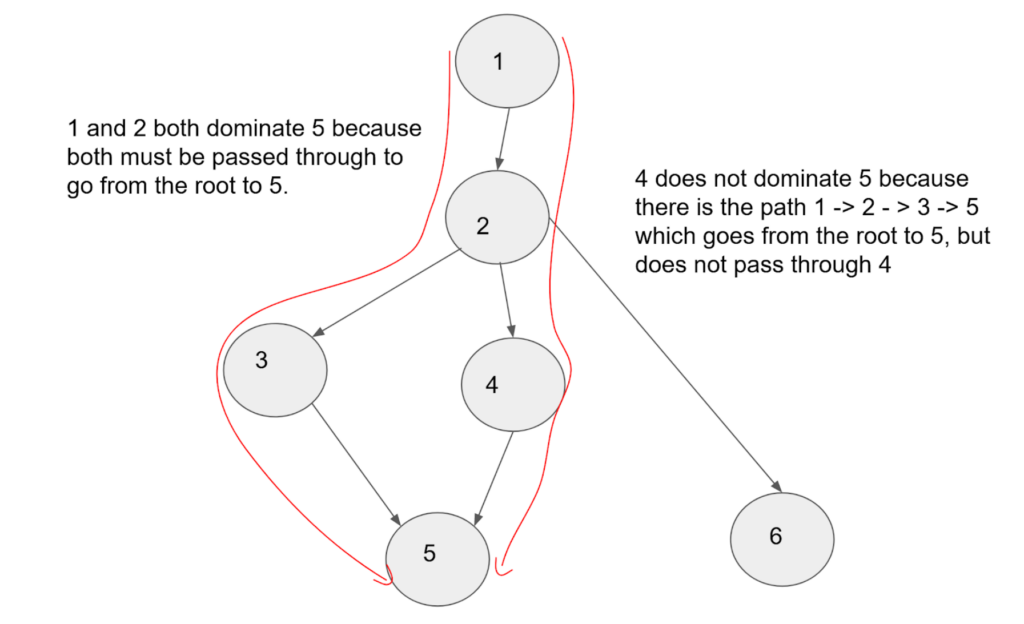
If u dominates w and v dominates w, Also, if u comes before v in the graph, then u dominates v (drawn below).

Algorithm for acylic graphs:
An acylic graph is a graph that has no cycle. Whether a graph is acyclic or not can be determined using one of the algorithms used to construct the topological sorting of a graph. If the topoloigcal sort does not include all nodes, then the folliwng method will not work. The immediate dominator of a node is the deepest node that dominates it (call this function dom(x)).
The following statement explains the process. dom(v) = lca(dom(u)) for every single direct path from u to v (v is the parent).
The LCA can be calculated using a strategy called binary lifting, which allows for LCA queries in O(log n). The following example should explain enough.
Refer to this slideshow that I made for an example on acylic graphs:
https://docs.google.com/presentation/d/11lFayqNbCSVmqloxO9pCkXrFpMAuCq9Ajf4m8EE_ZTI/edit?usp=sharing