What is the Newton-Raphson Method?
The Newton-Raphson Method is an algorithm to approximate the roots (x-intercepts) of a function. The method uses first derivatives and tangent lines to get an extremely precise approximation of an x-iintercept.
The Newton-Raphson Method:
Before using the Newton-Raphson method, the function that is being calculated must be known. A point will be randomly put on some point on the graph, and it will “roll” down the function until it reaches a root. The general algorithm goes as follows:
Put a point at some point on the graph and calculate the derivative of the function.
Using the derative, get the tangent line of the point.
Find the point at which the tangent line intersects the x-axis (call this point y).
Move the point to f (point y), and then repeat step 2 until the point becomes sufficiently close to the x-axis.
For getting the tangent line to a point, plug in the x value into the deriative. Point-slope is a representation of a line that only requires a point on the line and the slope. Plug the slope in and a point on the line, which would be the point that is going to be touched tangentially.
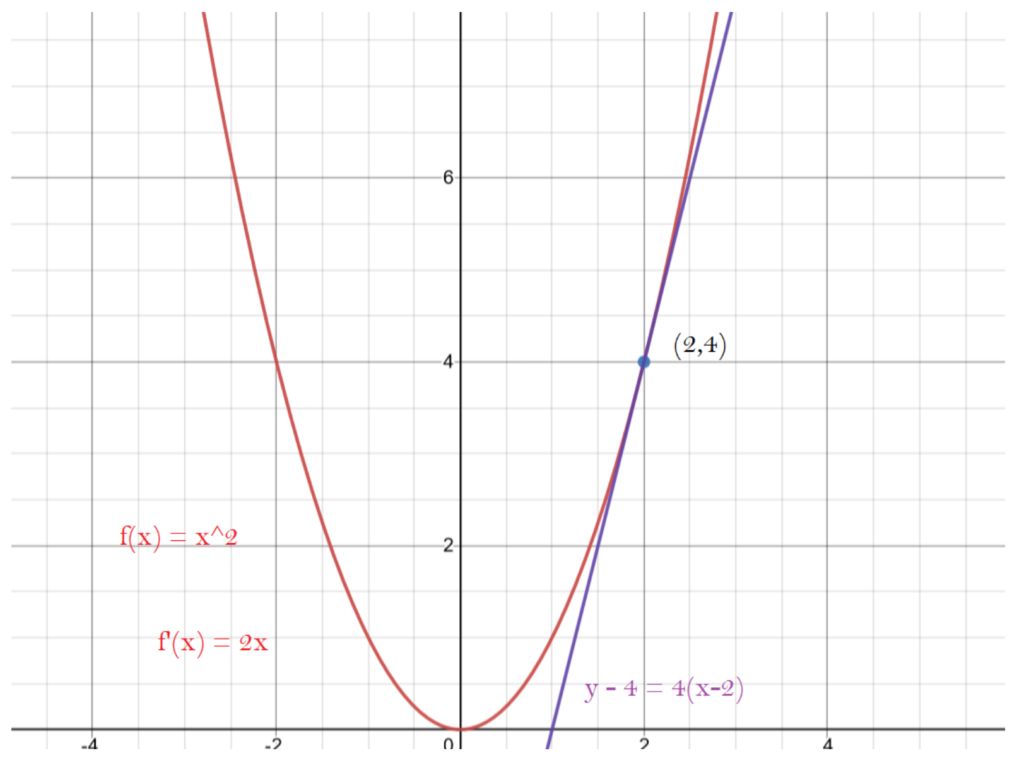
In order to find out where the line intersects the x-axis, put 0 for y in the tangent line equation. In the case of the above image, the next point to be tested will be (1,1). I currently don’t have a proof on hand, but all the steps will eventually lead to the following equation: Remember that f'(x) is the f(x) differential.
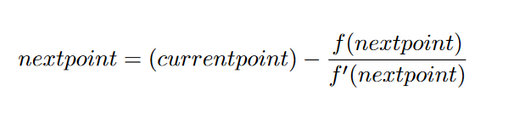
Here is a video explaining the Newton-Raphson Method (I do not own the video):