AVL Tree
Issues with a normal BST?
In order to be considered a binary search tree, the tree must have these properties:
- The left subtree contains nodes strictly less than the root node.
- The right subtree contains nodes strictly greater than the root node.
- Every node must maintain the top two properties.
It only makes sense that BST has O(log(n)) search time since you can choose whether to go on the left or right subtree depending on your values relationship to the root node.
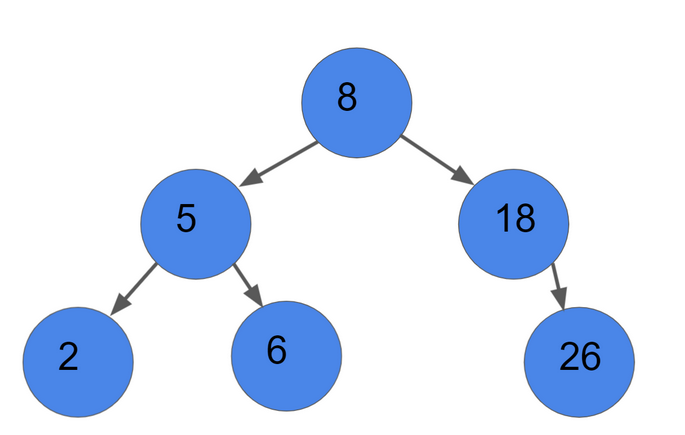
Example: Finding out if 6 exists
- Go to the left subtree since 6 < 8
- Go to the right subtree since 6 > 5.
- Return True, because your current node is 6.
You were able to find six without touching three nodes. It only makes sense for it to have a logarithmic time complexity.
Except, there are scenarios where the BST no longer maintains an O(log(n)) search. Remember, Big O implies the worst-case scenario. If you have a normal BST in that absolute worst-case scenario, it will take O(n) time to complete a search.
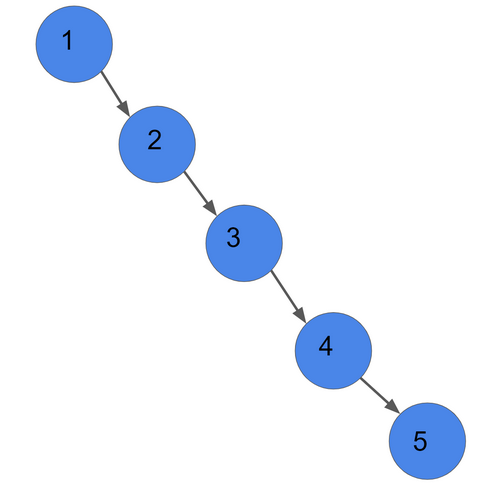
In the absolute worst case, the BST basically becomes a linked list. If you are searching for the number 5, Regardless, you must go in the order 1 -> 2 -> 3 -> 4 -> 5 to determine if it exists.
This type of tree is considered unbalanced. Scenarios like these lead people to develop self-balancing BST, so the search time remains O(log(n)).
The AVL tree invariant
An AVL tree is a form of self-balancing binary search tree. In order for a tree to be considered an AVL tree, it must first be a binary search tree, but it must also have a certain balance value. Balance can be calculated by the height of the left subtree and the height of the right subtree.
If the balance <= 1, then the AVL tree invariant is true at that point, and that tree or subtree is balanced. On top of proving whether the tree is balanced or not, The balanced value can also provide information on whether the tree is left heavy or right heavy, which will be important later.
Left heavy implies that the left subtree is dominant and can be determined as balanced > 0. Right heavy implies the right subtree is dominant and can be determined as balanced < 0.
BST, which satisfies the AVL invariant. Has a height of 3 and a balance of 1 at the root. In the image, we take an absolute value for the balance. If you didn’t do that, you would find that the balance was -1. Which implies a left-heavy tree.
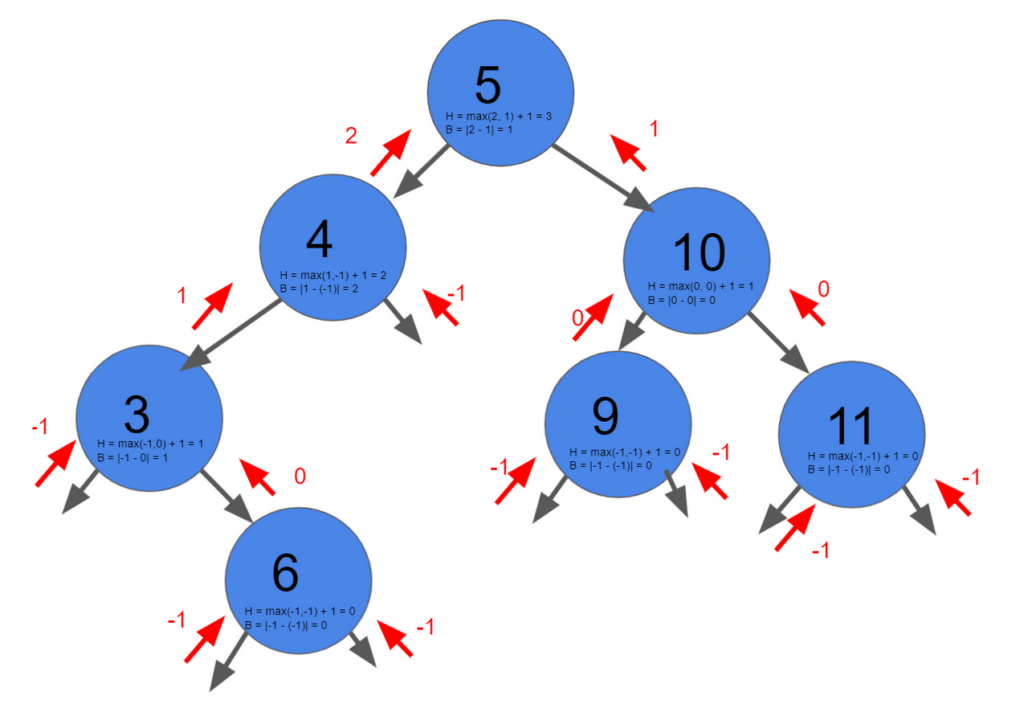
BST, which doesn’t satisfy the AVL invariant. Has a height of 4 and a balance of 2 at the root. Due to the fact that balanced is greater than 1, it cannot be an AVL tree. In the image, we take an absolute value for the balance. If you didn’t do that, you would find that the balance was -2. Which implies a left-heavy tree.
Side Note:
Height is calculated as the number of edges between that node and its chosen ancestor. This means a null node has a height of -1 and a leaf node has a height of 0.
AVL Tree Rotation:
There are four different types of AVL tree rotations. Which rotations you will need to use are based on whether the tree is left heavy or right heavy.
Left Heavy Trees:
- Right rotation
- Left-Right rotation
Right Heavy Trees:
- Left rotation
- Right-Left Rotation
If your tree is left-heavy, it only makes sense to move more items to the right side, which is why you would do a right rotation.
Time Complexity:
Search = O(log(n))
Deletion = O(log(n))
Insertion = O(log(n))
Space Complexity = O(n)