Introduction
The Pade approximant uses rationals in order to approximate functions. The Pade approximant tends to be better than the Taylor series when it comes to approximating functions. When using Taylor series, the approximate function seems pretty close to the real function initially, but then at some point it shoots off to infinity on both sides. That is due to the nature of the Taylor series, which uses polynomials. In both Pade and Taylor approximations, the higher terms will eventually take over. However, polynomials grow much faster than rationals, so a Taylor series will become an invalid approximation almost instantly once that threshold is hit. While a Pade approximation will grow much slower and follow the behavior of function, Refer to the image below, which shows a Pade and Taylor approximation of a sine wave.
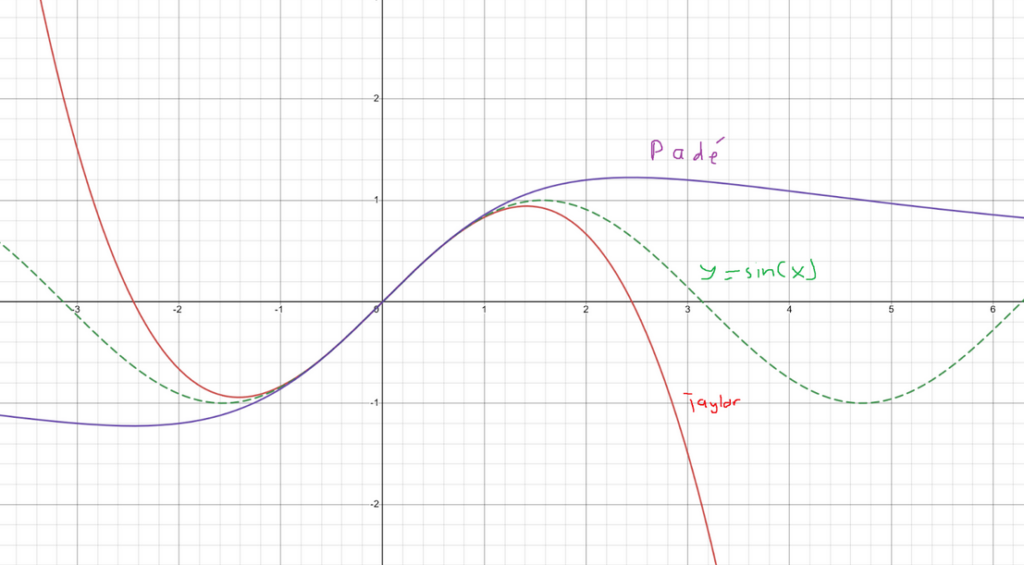
As soon as the Taylor series reached about 1.5, it completely shot off to infinity on either side, while the Pade approximation stayed much closer to the original function. The Pade approximation is still far from right, but it won’t yield outrageous values. With this certain Pade approximation, the denominator has higher terms, and the approximation converges to zero on both sides.
An [N/M] Pade approximant is constructed with an Nth-degree polynomial in the numerator and an Mth-degree polynomial in the denominator. The values of N and M will change the end behavior of the approximation, and they have the following general form:
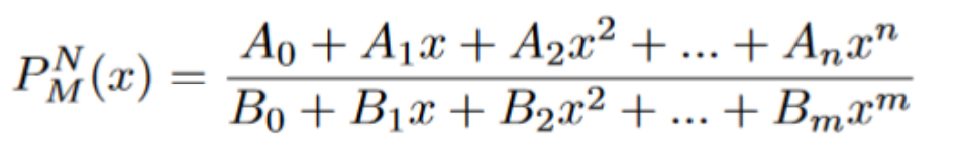
The Pade approximant will agree with the Taylor Series approximation for the first N+M terms. For an example, I’m going to show the process to approximate a sin(x) using a [2\2] Pade approximation. Our [2/2] approximation will be equivalent to the first two terms of the Taylor series of sine, which will be useful for determining coefficients. We also know that B0 must be equal to one in order to comply with the Taylor series.
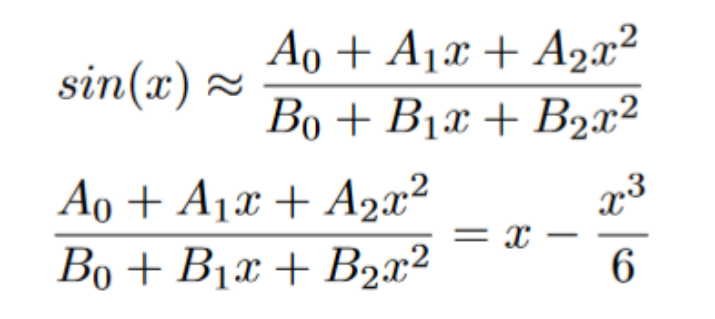
If we multiply by the denominator on both sides of the equation, we will get the following:
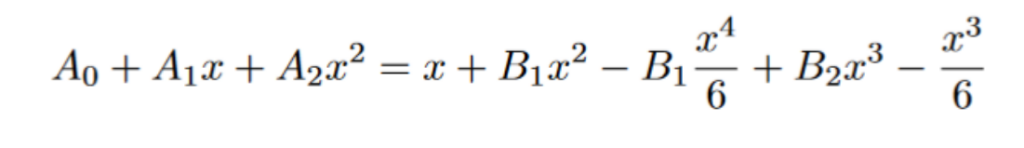
Matching the values across the equal signs, we get that:
Ao = 0 (since there are no constants on the right side of the equation).
A1 = 1 (in order to match the linear coefficients).
A2 = B1 (matching quadratic coefficients)
0 = B2 minus (⅙) or B2 = ⅙ (matching cubic coefficients)
0 = -(⅙)B1 or B1 = 0 (matching coefficients)
Plugging the values we just obtained into the Pade approximation, we get the following rational function:
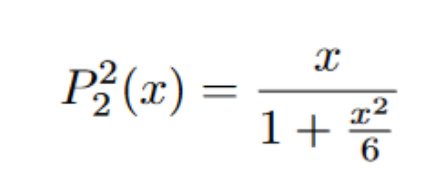
This function is the exact same one used in the first image. As mentioned prior, the function will approach zero on both sides, contrary to a Taylor series, which would explode towards infinity. Due to how Pade approximation deals with end behaviors, many people prefer to use Pade approximation over Taylor approximations.