Introduction
When describing fluids we typically use density instead of mass. Density is defined as unit mass over unit volume. The formula for density is listed below (measured usually in kg per meters cubed)
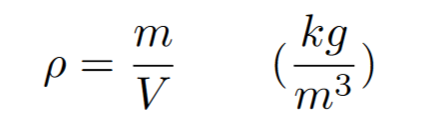
Pressure is another important value in fluid mechanics and it is defined as force divided by area. Pressure goes up whenever more force is applied or the area by which the force applied shrinks.
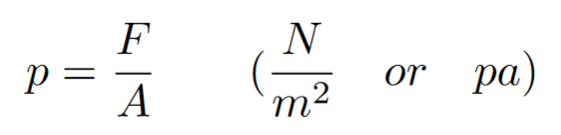
Fluids will apply pressure in every direction. The deeper you go a fluid the more the fluid is above you so there’s more weight pushing down. That’s why your body feels compressed when you stand at the bottom of a deep swimming pool. The formula for pressure mimics the formulas you might see in classical mechanics (except with density replacing mass):
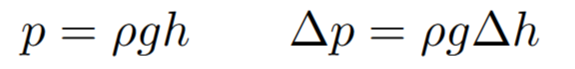
Pascal’s Principle
The water in a pool is an example of confined liquid. Pascal found out when you apply pressure to a confined fluid the pressure in every part of that fluid increases by that same amount. The principle is called “Pascal’s Principle”.
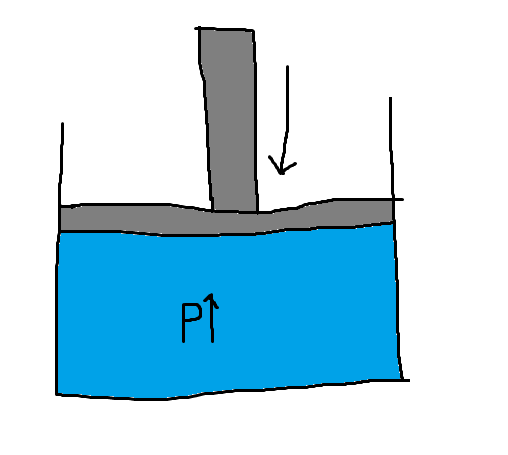
Pascal’s Principle is extremely useful and is the core principle involved in the functionality of hydraulic pistons. Let’s say you have a piston like in the figure below. If you apply a pressure (by applying some force) on the left the fluid will push the opposite side of the tube with the same pressure.
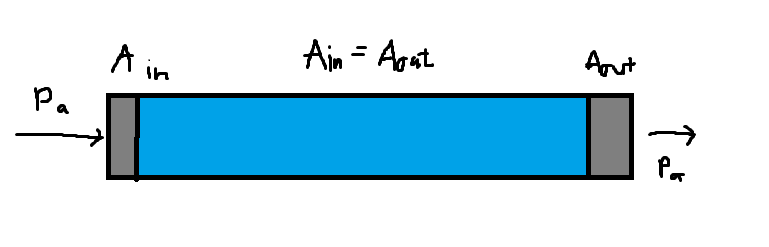
If the cross sectional areas of each side of the tube vary then the force experienced on each side will be different (remember that pressure is force divided by area). Therefore, if you apply a force on the left side and the right end of the tube has a higher cross sectional area then the right side will actually be pushing out with more force than what was originally applied on the left. The fluid is confined and the system is in hydrostatic equilibrium meaning the following conclusions are true.
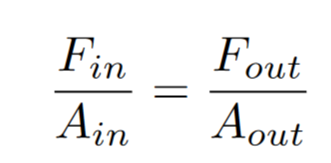
The above equations can be applied to scenarios such as the one below.

The idea of a hydraulic press is to have the force applied side have a significantly smaller cross sectional area than the right side in order yield a much greater force as an output.

Manometers and Barometers
Manometers and barometers are devices used to measure pressure.
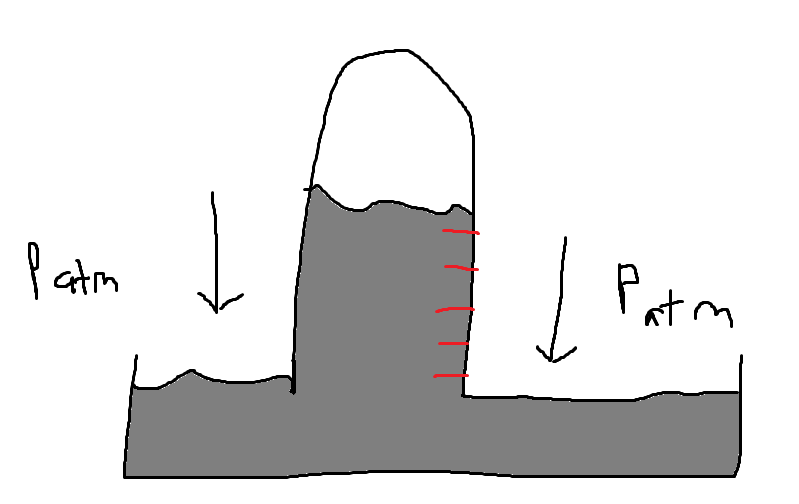
In a manometer, one side of the device is connected to an object, such as a bike tire, while the other side is open to the atmosphere. The side with higher pressure will exert more force on the liquid (typically water) in the manometer, causing the liquid to rise on the other side. The change in the height of the liquid can then be used to calculate the pressure difference. In this system, two types of pressure are present: gauge pressure (such as the pressure in the bike tire) and atmospheric pressure. The total pressure in the system is the sum of these two values.

When measuring the pressure contributed by something like a bike tire using a manometer, we can utilize the equation for pressure mentioned earlier. By measuring the change in height of the water in the manometer (Δh), we can use this value in the equation to determine the pressure.
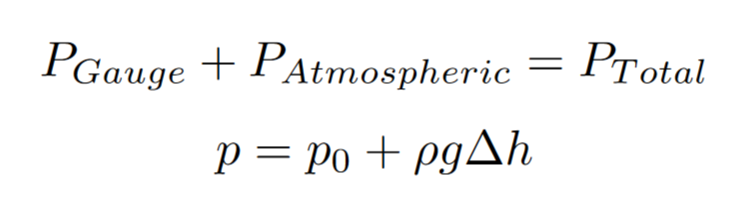
On the other hands Barometers measure pressure using mercury. A barometer is made up of an upside down tube which has tick marks and a bowl of mercury at the bottom. Atmospheric pressure will keep a certain amount of mercury in the tube. As pressure goes up in the system so does the mercury in the tube. Pressures measured from barometers usually have units of millimeters of mercury (mmhg).
Archimede’s Principle
Archimedes’ principle states that the volume displaced by an object is equal to the object’s volume. Through the use of a little manipulation Archimedes principle allows us to connect the rise in water level in a fluid to the volume of the objects that are contained inside. All we need to know is the cross sectional area of the tub of water.
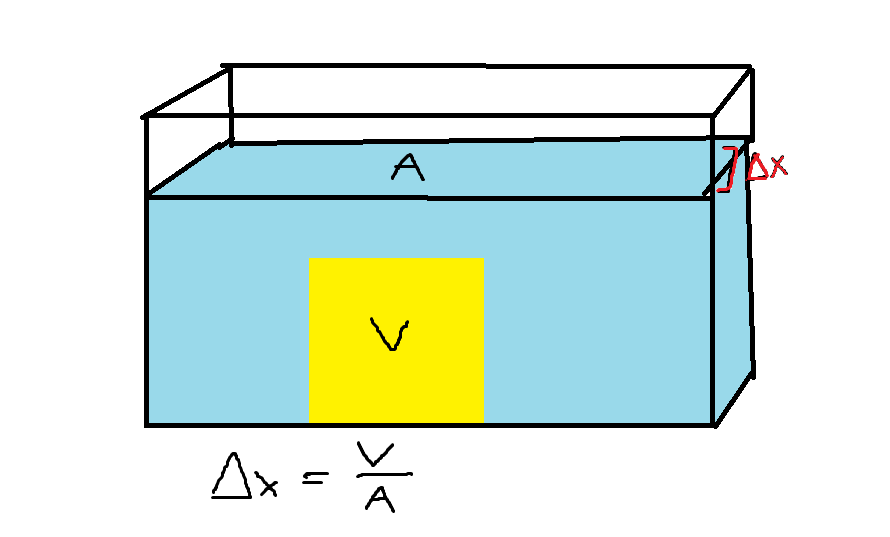
Beware that this is only the case when the object is fully submerged. If an object is floating and is partially above the water then the portion that is above the water doesn’t contribute towards the volume of the water that is displaced.
Buoyant Forces
For a non-moving object in a fluid it experiences two different forces. A buoyant force and a gravitational force. After some time the object will reach an equilibrium where the forces are equal to each other and it will stay still in the fluid.
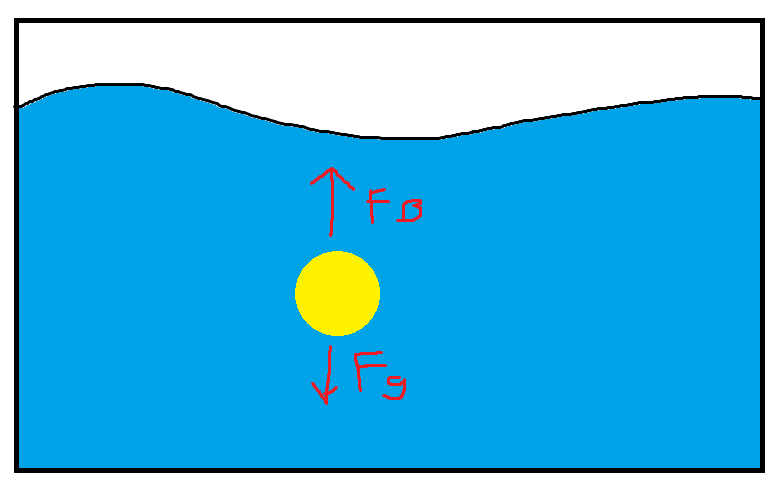
Buoyant force is caused by the fact that water pressure is greater at the bottom of an object than at the top of an object.
When you put a bunch of objects of equal shape and size, but with varying density then the most dense object will sink. The buoyant force will remain the same as a result of the shape/size, but the dense object will way more and therefore feels a greater gravitational force causing it to sink. The equation for the buoyant force is written in either of the following ways (2nd way is generally more useful and is Archimedes’s principle):

If an object has so little density that it partially floats the buoyant force will go down as less fluid is being displaced. Air is a fluid and does have a buoyant force but its contributions are so small that we choose to ignore it in almost every case.
Fluid in Motion
Firstly two important definitions:
Incompressible Fluid – Density remains constant
Laminar Flow – Fluid flows smoothly (do not need to take viscosity into account)
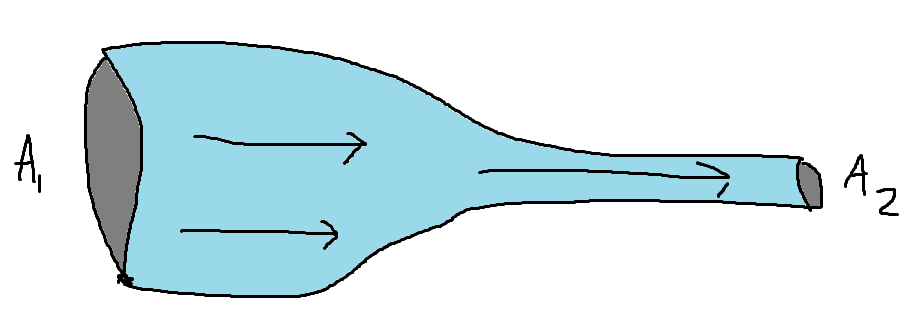
When a flow is laminar it allows for a lot of the math to simplify. In a pipe containing a smoothly flowing fluid whenever the pipe’s cross sectional area decreases, multiple properties about fluid will change. However, one thing that won’t change in the system is the amount of mass flowing through the pipe (Mass Flow Rate). In order for the same amount of water to push through a smaller cross sectional area the water needs to be moving faster. That can easily be achieved because as water flows into the smaller section it receives the same amount of force from the water behind however, it’s concentrated causing the water in front to speed up

Also, through some manipulation we can solve for a rough relationship between the two different parts of a pipe. First, consider the definition of density and then solve for the mass.
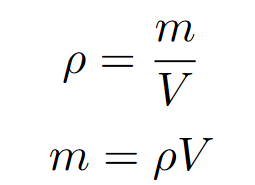
We can then differentiate the equation of both sides to yield the following:
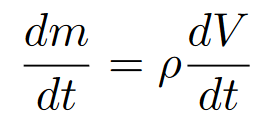
It also important that we can recall some of other formulas such as the following (these should be pretty intuitive if you think about them):

Substituting in the equations for change in volume and velocity we then get:
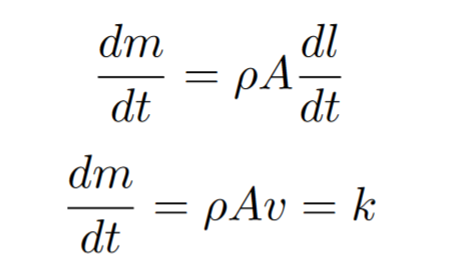
Through continuity we know that the rate of change of mass with respect to time is always some constant meaning that the following is always true:
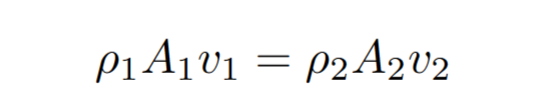
The above equation allows us to compare the densities, cross sectional areas, and velocities of two different parts of a pipe. For an incompressible fluid the density is constant so our equation can be reduced to:

Bernoulli’s Principle
Bernoulli’s Principle states that the higher a fluid’s velocity is through a pipe, then it exerts a lower pressure on the walls of the pipe, and vice versa.
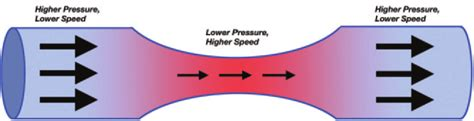
Bernoulli’s Equation
Bernoluii’s Equation is based on the conservation of energy. He sums all properties of a fluid such as pressure, kinetic energy, and potential energy. Since, is conserved he knows that all of that must equal some constant.
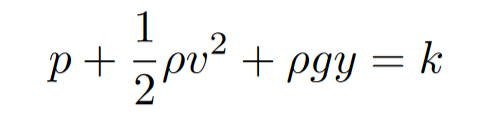
Since the constant is shared everywhere throughout the tube we also get the following equation that allows us to compare two different parts of a pipe:
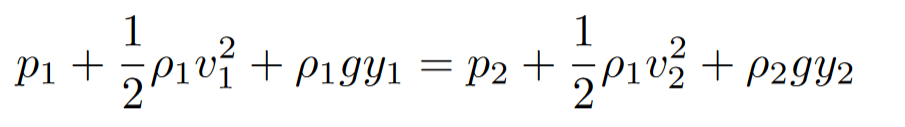
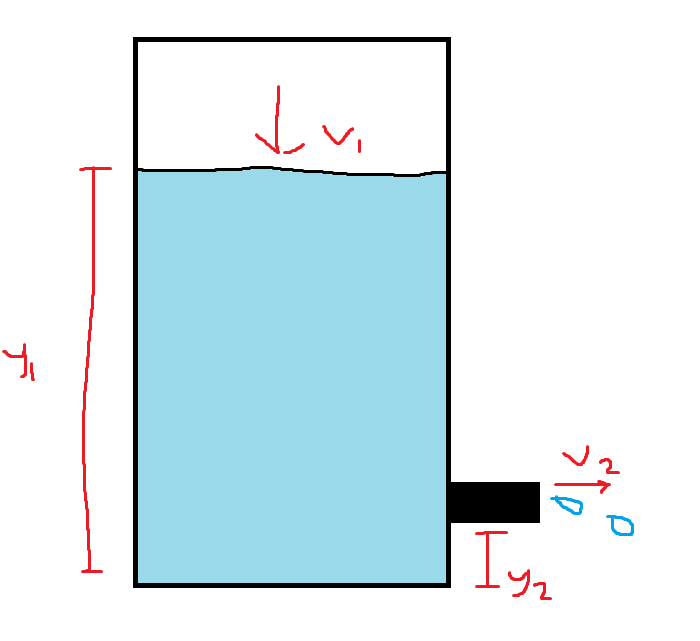
Torricelli’s Theorem
Torricelli’s Theorem states that the velocity of fluid coming out of a spout is the same as the velocity of a single droplet of fluid that falls from the height of the surface of the fluid in the container. The system has a setup similar to that of what is shown below.