What are Wavelet Trees?
The two common problem statements:
- Given an interval [L:R] find how many times some value X occurs
- Given an interval [L:R] find the kth smallest number
Construction of wavelet trees
Segment trees are constructed with indices, while a wavelet tree is constructed with values in mind. The image depicts how the tree will be constructed. When a wavelet tree excludes certain items, it remains stable. This means that there might be stuff missing, but the original order still holds (also called a subsequence). For an array [1, 2, 3], [1, 3] is a stable operation, while [2, 1] is not.
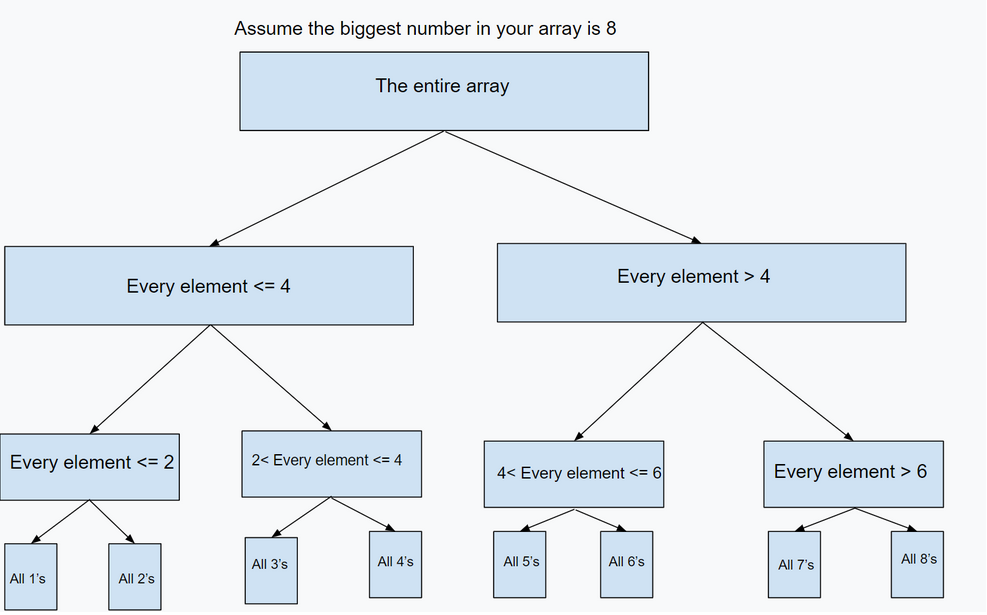
Pivots / Choosing Middle Values
Every time the node is split it is cut into two parts. At every node a middle value is calculated. It is very similar to binary search. 8 / 2 = 4 so, that is why it is split that way at the first level. For the node “Every element > 4” the remaining number of values to be searched is four (think about binary search, you already eliminated 1-4).
So, (previous middle value) + (remaining values to check // 2) = (The new middle value). This will yield 4 + (4 // 2) = 6. Which is why the pivot is 6.
Some Dynamic Programming
In order, to optimize for time complexity for queries on each node of the wavelet tree there will be an array recording how many numbers are greater than the middle value. The program will simply keep a running sum of the amount of numbers which are less than the middle as shown below.
The array allows the program to figure out where it is at any point in constant time. In the wavelet tree some values might be missing because it is constantly splitting them up. Example shown below:
First Problem: Given an interval [L:R] find how many times some value X occurs
Lets say that the current input gives the interval [3:7] and the value 2. At each node the data structure will make the decision to either go right or left. If the number it is searched is greater than the mid value it will go right and it will go left otherwise. As items are seperated the interval saying that it goes from 3 to 7 is no longer true in the new node since stuff was “removed”. The trick mentioned right above this is used to determine the adjusted interval in O(1). This will continue until the node which holds X only is reached.
Second Problem: Given an interval [L:R] find the kth smallest number
This is very similar to the previous problem. In the previous example, it eliminated all of the values which weren’t the one specified value. If the there isn’t enough items the it will go to the right if there are two many items that abide by the rules it will go left. In this problem, the query will keep going until there is a “split decision” in the tree. The query is obviously aiming to reduce the interval to a length of K.But, if the array has a length of K there is no way to determine the maximum without searching through it. So, the query will continue until it has a decision where one route means the k-interval will be too small and the other will make the interval bigger than k. In that case, the answer is simply the middle value being at that point.