What is a suffix array?
A suffix array is a data structure used to replace many of the operations supplied by a suffix trie while using less space. The suffix array is a lexiographically sorted list of all suffixes of a word. The suffix can solve the longest common substring (LCS) and longest repeated substring (LRS) in optimal time. Many problems can be reduced down to some of the fundamental problems suffix arrays can be used on. Suffix array of “burger” on the left
Remember that a is lexiographically smaller than aa. When there are no more tie breaks by letters, the smaller word is always first. Thus, the picture on the left is wrong.

Longest Common Prefix (LCP):
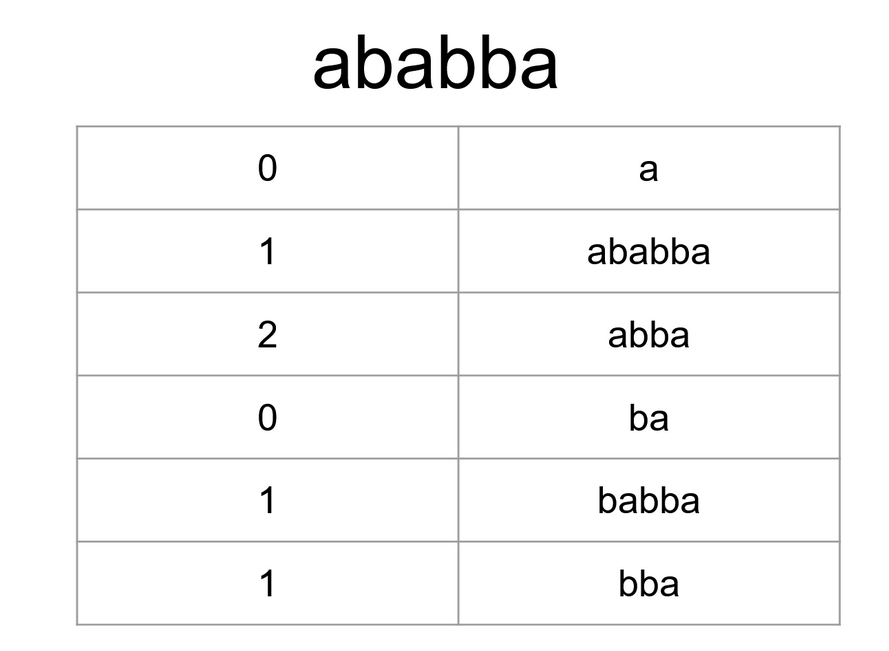
A lot of the functionality that comes from the suffix array comes from the longest common prefix (LCP). In a suffix array, this is calculated between adjacent values. Due to the fact that the suffix array is lexiographically sorted, it is being compared to the closest string lexiographically. For each index x, it is compared with index x-1. Then the maximum prefix between the words is calculated. -+ For convenience, since the first node does not have an x-1 value, it has a LCP of 0. Below is the following LCP/Suffix table for the string “ababba”. The LCP gives a lot of information about the string.
Longest Repeated Substring (LRS):
The longest repeated substring is the longest substring that appears multiple times in the string. The substrings are allowed to overlap. The LRS of “aaa” is two; it has two “aa” inside of it. Finding the LRS in a suffix tree is very simple. Try to find the LRS of the previous image and observe the value in the suffix array. The LRS is simply the biggest LCP value in the suffix array. According to the table, the LRS of “ababba” is “ab”. That means with a suffix array, the LRS can be calculated in O(n).
Finding Unique Substrings:
The title of the problem is pretty self-explanatory. All unique substrings of “aba” are [a, ab, aba, ba, b]. The standard O(n^2) would have first produced all substrings [a,ab, ba, ba, a] then removed any duplicates. By the way, remember that there are (n^2 + n)/2 substrings in a string. (n^2 + n) /2 is the same as the sum of 1, 2, 3,… The LCP in the suffix array prevents us from calculating possible duplicates.
For clarification, there will still technically be “duplicates”. But the indicators that are used are different. So, in abab,” “ab” made from 0 and 1 is considered different from “ab” made from 2 and 3. Duplicates in terms of actual values still have to be controlled with a hashset or a similar technique.
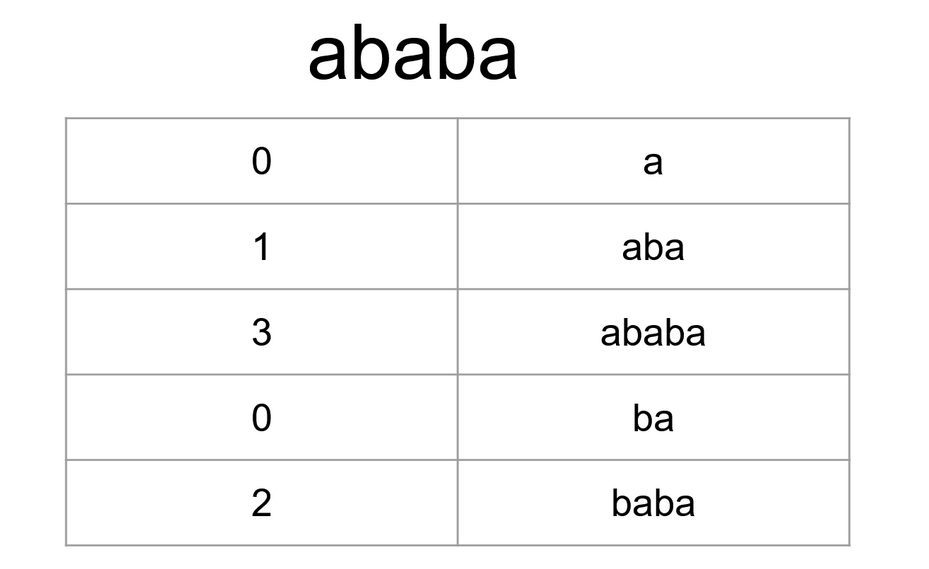
Observe the LCP for the following string: “ababa”. The general idea of how all substrings work is still brute force, but it is optimized. Between “a” and “aba” they both share “a.”. If calculating the order of the suffix array, then the first letter doesn’t need to be calculated, as it was already done in the previous step. Between “ababa” and “aba” they both share “aba”. So, the substrings produced strictly from letters 1-3 in Ababa aren’t of any use since they were already done in the previous substring.
For example, when calculating the substrings between aba and ababa, the following substrings need to be generated (0 indexed):
Each substring isn’t necessarily unique, but the indicators used to make them always are.
[0,3] abab
[0, 4] ababa
[1,3] bab
[1,4] baba
[2,3] ab
[2,4] aba
[3,3] b
[3,4] ba
[4,4] a
Longest Common Substring (LCS):
This is the most complicated of the three main problems that a suffix array can solve. In this problem, there are multiple substrings, and the algorithm will find the longest substring that is contained in all of them. As an extension of the problem where only k of the substrings need to have a common substring, If all substrings must have it, then k = the number of substrings. Firstly, concatenate all of the substrings together with a delimiter like #, $, or %. So, if given “bcdb”, “cdbe” and “ebdb” are presented, then a valid concentation can be “bcdb#cdbe#ebdb”. It’s important to separate the value from the substring so it’s not included in any of the substrings. Now construct a suffix array out of them.
Also, try to color each substring. Catergorize each substring into the most recent substring that isn’t finished. This can be calculated by figuring out how many delimeters have been passed before adding them. This information will be used later to figure out if enough different substrings satisfy a certain constraint.
The first (# of substrings in this case) values in the suffix array don’t need to be considered because they start with a character that was not originally in any of the words. The sliding window technique and hashtable can be used to run this algorithm effectively. Sliding windows have many applications outside of suffix arrays.
General Algorithim:
Initialize a window that is of length k. Add the amount of each color in the current window. The values in the hashtable will determine if at least k different substrings are being considered. I also calculated the LCS. The longest common substring is the minimum of all of the LCP values present in the window.
Then, repeat these cases until you reach the last index and shrink the window. (Some of these might not be resolved in one operation, so each will be on a while loop.)
If there are more than k colors (colors > k), First, compare the LCS to the current best answer, as it is valid. Then move the left pointer to the right, shrinking the window. Adjust the hashtable and the LCS by figuring out the minimum LCP.
If exactly k colors (colors == k), First, compare the LCS to the current best answer, as it is valid. Then, move the right pointer to the right, expanding the window. Adjust the hashtable and the LCS by figuring out the minimum LCP.
If less than k colors are present in the window (colors < k), Do not compare LCS to the best answer, as it is not valid. Then, move the right pointer to the right, expanding the window. Adjust the hashtable and the LCS by figuring out the minimum LCP.
How the minimum range queries for LCP can be done with a segment tree or something can probably be done with a second hashtable.