What is Johnson’s algorithm?
Johnson’s algorithm is an edge reweighting technique. Johnson’s usually works to change negative-valued edge weights to positive edge weights. This allows the standard non-negative graph algorithms to work. Johnson’s algorithm doesn’t work when a negative cycle is present.
Johnson’s Algorithim:
Johnson’s algorithm makes use of the Bellman-Ford algorithm to deal with the negative weights. Johnson’s algorithm also uses an artificial node. Johnson’s algorithm goes as follows:
Create an artificial node that points to all of the other nodes in the graph with a weight of 0. Call this node X.
Now use a single-sourced shorest path algorithm starting from node X. Due to the existence of negative edge weights, the Bellman-Ford algoithim must be used instead of dijkstras.
Bellman Ford, if you forget (neither are my videos, sourced at the bottom): https://www.youtube.com/watch?v=obWXjtg0L64 or https://www.youtube.com/watch?v=lyw4FaxrwHg . Now all of the shorest paths for each node from s are 0 or less than 0.
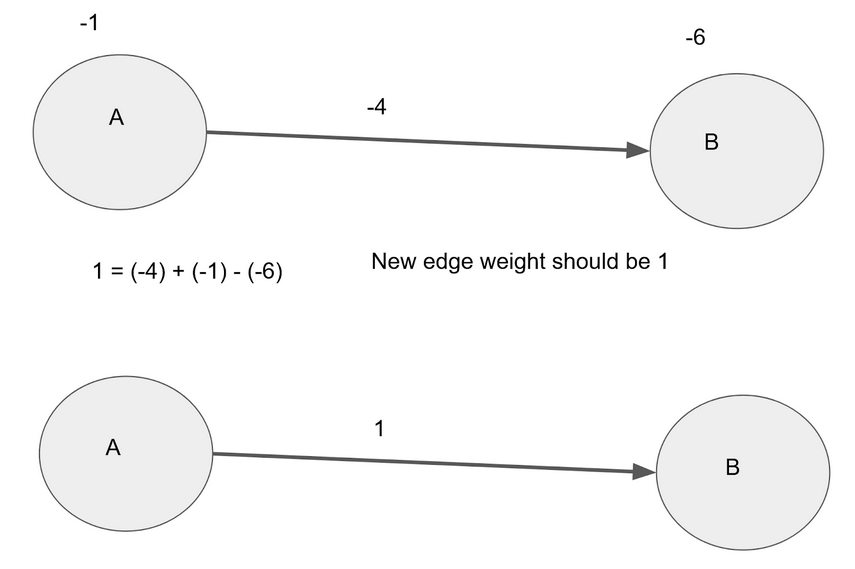
Now go through each edge and use this equation to calculate the new edge weight:
new edge weight = (current edge weight) + (starting node shortest path) – (ending node shortest path)
Now the graph only contains positive values, allowing for the standard positive edge weight algorithms to be used. Dijkstras can now be used to do a single-source shortest path, and Floyd Warshall can be used to do an all-source shorest path.
new edge weight = (current edge weight) + (starting node shortest path) – (ending node shortest path)