Graham and Jarvis Methods for Obtaining a Convex Hull
The Graham scan and Jarvis march are both algorithms used to construct the convex hull from a set of points. They both rely on finding points that are all going in the same direction.
Cross Product Between Vectors:
G.S. and J.M. both rely on finding points that all go in the clockwise direction. This can be determined by using the cross product of vectors. The cross-product of vectors can be determined by:
u x v = |u| |v| sin( angle between the vectors)
If the cross product of the two vectors is positive, that means that the two vectors have less than 90 degrees of freedom. If the cross product is positive, the point is going clockwise to the previous node. If the cross product is negative, that point is going counterclockwise to the previous node.
Graham Scan:
In Graham, a stack is used to maintain the order in which the nodes are processed. Description of the algorithm:
Find the point with the lowest y-coordinate and put it in the stack. Also, go through the other points, recording the angle with the lowest y-coordinate point.
For the point at the top of the stack, iterate through the rest of the points in counterclockwise fashion. When a clockwise turn with a point is made, add it to the stack.
After adding it, go to the new node and repeat step 2. If the point only makes anticlockwise turns, then pop in from the stack. Continuing the search on the point that came before it, basically repeating step 2.
Once the search returns to the point with the lowest y-coordinate, it is done. The stack contains the nodes, which are the points of the convex hull.
Jarvis March:
Jarvis March takes on a more brute-force method for finding convex hulls.
Find the point with the lowest y-coordinate, just as in the Graham Scan.
Now loop through the rest of the points in a specific order. After the iteration, create a side of the convex hull by connecting the current point to the point that makes the smallest counterclockwise turn.
Continue until you reach the starting node.
Here is a youtube video explaining both the Jarvis March and Graham Search (I do not own this video):
What is a Li Chao Tree?
A Li Chao tree is a dynamic segment tree data structure that is commonly used for convex hull problems. It is a replacement for the convex hull trick. As nodes, it doesn’t store an integer value but a line. It’s best explained with a question prompt.
Question Prompt:
Create a data structure that supports two queries:
Add a line y = mx + b (m = slope, and b is the y-intercept).
At some point, get the minimum value that is on one of the lines.
Naive Approach:
Since every line is present at every x value, simply evaluate all lines at x and get the smallest.
The Li Chao Tree Data Structure:
The Li Chao uses the idea of a dominant line. In Li Chao Trees, which is a segment tree, the root value covers the dominant line over [l:r]. The right child of the root is responsible for the dominant line over [r/2, r]. The left child of the root is responsible for [l,r/2).
The LC tree cuts the interval in half. The dominant line is the line that must be considered both on the left and right sides of the line that cuts it in half. Remember that the question asks that we return the minimum value? In this case, blue is the dominant line. The green line is the line that will be used as the value of the root.
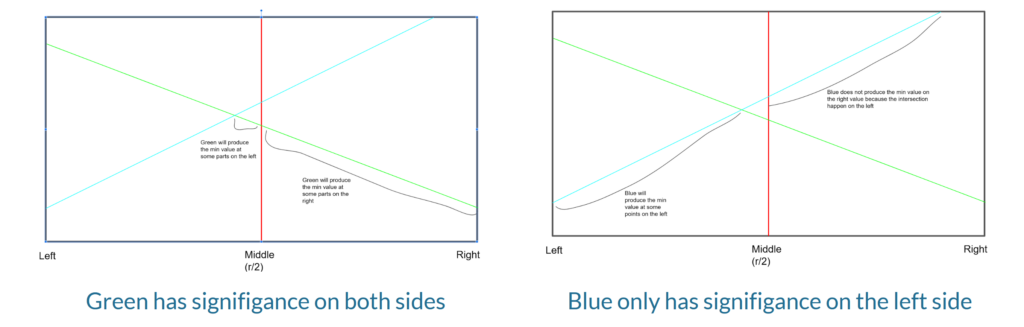
This process of finding the dominant line will continue. Below are pictures of how the root’s left and right children are determined. A new middle is established. This process will continue until the interval has a length of one.

Querying the Li Chao tree:
The Li Chao allows the number of possible answers to be reduced. In order to query a Li Chao tree for the line that will produce the lowest y coordinate at some x coordinate, follow these steps:
Use the intervals of each node to navigate where x is located in the Li Chao tree.
Example: If the node currently stores the interval [1, 10] and the x value is 3, then it is clear that the left subtree must be explored. This is because the segment tree is split in the middle. The left side stores [1, 5], and the right side stores (5, 10).
While going down towards the x-coordinate value. Evaluate each line that is touched when trying to get to the correct x-coordinate. Once the position is finally reached, return the smallest amongst them.