Problem Descirption:
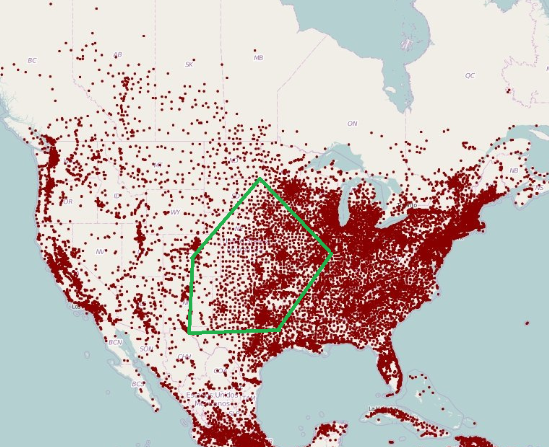
I do not own the original piece. On the right, here is the source: https://valuewalkpremium.com/2018/10/mapped-population-density-with-a-dot-for-each-town/.
The image on the right is a map of towns in the United States. Each red dot is a single town. There is also a convex polygon on top of the map. Some people ask how many towns are located on the inside of that given convex polygon. Is there a good way to find this information? That is where simplex range searching comes in.
It can also be done with non-convex polygons, but that will be talked about later.
Simplex Range Query:
Currently, the problem is extremely complex. For this type of query, dealing with the entire convex polygon at one time is a poor idea. In order to do this task, the convex polygon needs to be broken up all the way to its simpliest form. Every simple polygon (not self-crossing) can be triangulated. Now that it is split into a bunch of triangles, is it possible that it can be reduced even more? Each triangle contains three line segments. In our case, it’s best to interpret them as half-planes. These are lines that contain all the points on one side.
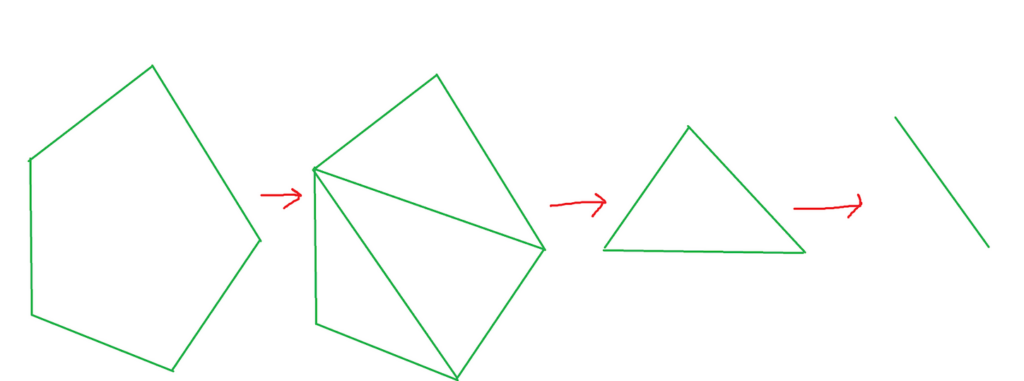
More Information
Now that the search space has been reduced to a bunch of small problems, To determine the number of points inside a triangle, we take its three half planes and then find the intersection of those points. Now that we know all of the answers to each individual triangle, adding up all of them will give the answer to the entire convex polygon. The points that will be counted in a triangle are the points that would exist in the green, red, and blue regions at the same time.
Our current problem is: how do we find how many points are in the shaded region of the half plane of a triangle?
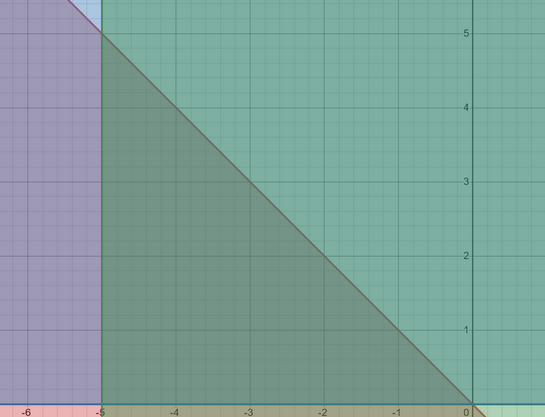
The 1D scenario:
I do not own the image on the left. The image is a screenshot from the following video: https://www.youtube.com/watch?v=cqGYokABuDg&list=PLubYOWSl9mIvTio-1bXWnhE9LdeXfox1z&index=52
The 1D scenario involves drawing a number line and finding the points that are greater than a certain value. To have a dynamic system, a balanced binary search tree should be used. Each point on the number line will have a point in the BBST. On top of storing the value of each point in the number, each node will also store the number of nodes in a subtree. When a query value is given, all the node has to do is find the closest location in the BBST, then just check how much is in the subtrees to the right of it. The 1D scenario isn’t very hard, but it is important to understand the 2D scenario. This will yield an O(log n) time complexity.
The 2D scenario:
Our issue still lies with how to calculate how many points exist inside a halfplane.
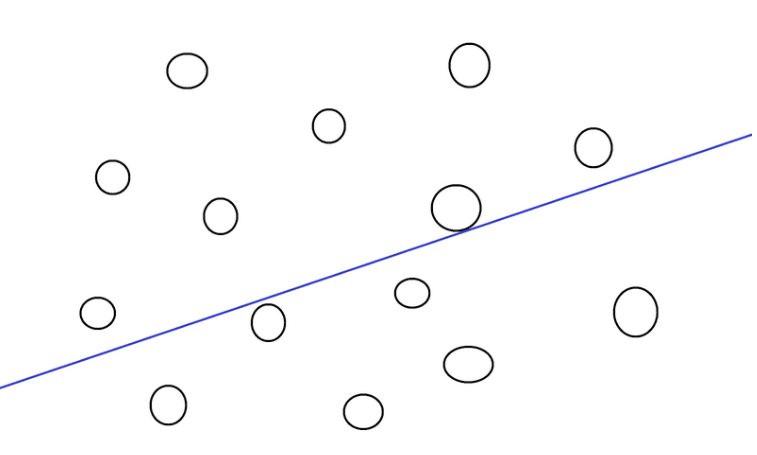
Assume the following data points exist: The blue line represents the half plane, and the query wishes to find how many points are above the blue line. This problem is most likely complex currently, so it needs to be broken down.
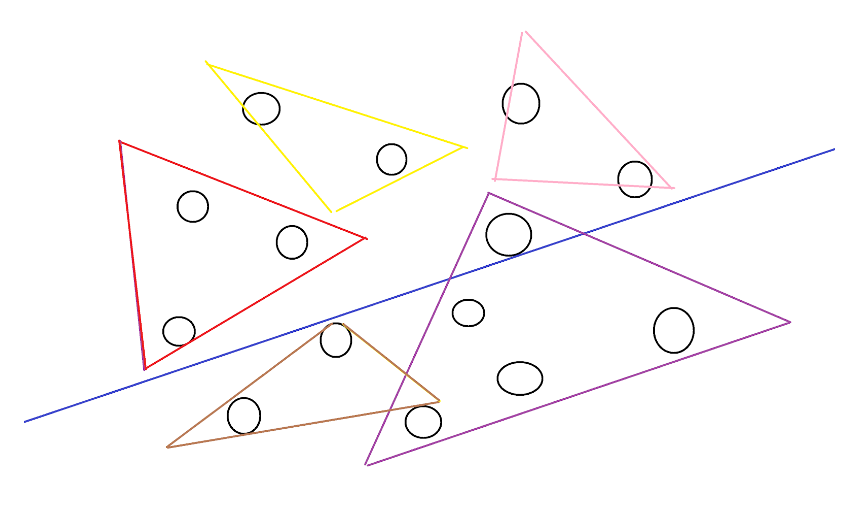
The triangles don’t stop there. Each of the points exists inside a triangle as well. This allows us to cut down on operations. If we know that the red triangle lies completely above the purple line, then all of the nodes contained inside the red triangle must also However, the purple triangle intersects the line.
The solution to the purple triangle intersecting the line is to just create subtriangles inside the triangle that already existed. Now we know that the three points in the orange triangle lie below the line, and the green triangle with one node also lies completely under the line. The light blue triangle lays completely above the line, meaning it should be counted in the answer.
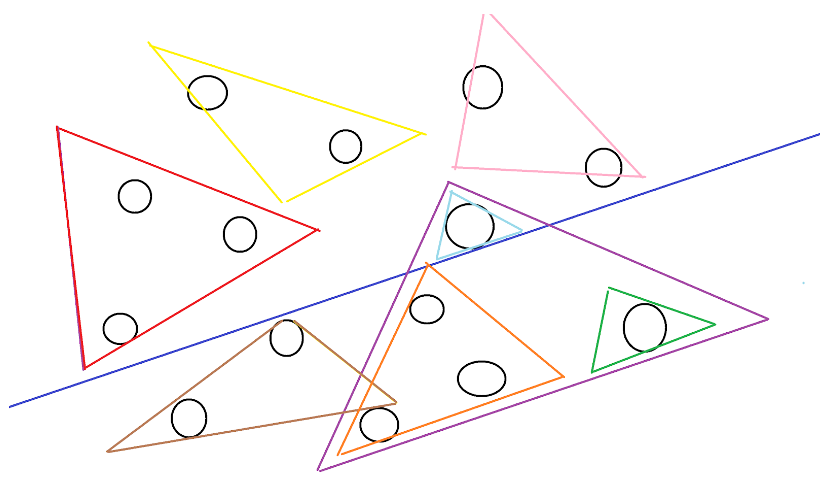
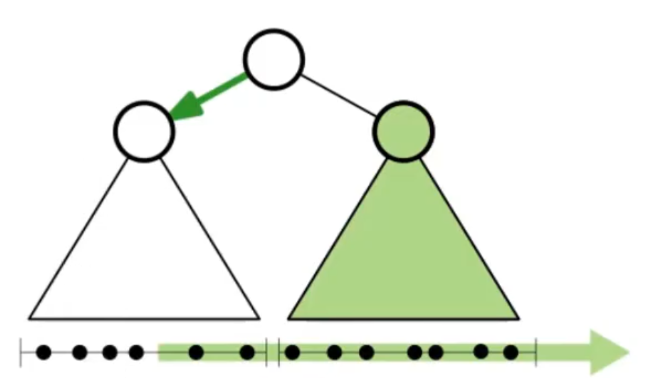
The general idea to reduce starts with big triangle groups. Then, recursively, make them smaller until there is just a single point. This method attempts to break up the work so calculations can be simplified. All of this information is stored inside a data structure called a partition tree.
In a partition tree, the immediate children of the root node are the biggest triangles. Then, all of their children represent the smaller triangles that make up itself. As the tree is traversed, the size of the triangles gets smaller and smaller until a triangle with only one point is reached. The algorithm for querying is very similar to how the triangles were constructed. The steps go as follows:
- Look at the partition trees and find the triangles that lie entirely above the line.
- If the triangle intersects the line, then the subtriangles need to be consulted. Then, repeat step 1 for the smaller triangles using the new smaller triangles.