Problem Statement:
There is an art gallery where there are a lot of thieves. The art gallery is in the shape of a simple polygon. Your job is to place cameras so that the entire polygon is covered. The camera can look in a full 360 degree, but it cannot look through walls. The museum obviously wants to minimize the number of cameras. Attempt to cover the museum while using as few cameras as possible.
Solving the Art Gallery Problem:
The problem is extremely complex in its current state. When we have a “complex” simple polygon, it may make it hard to calculate good places to put a camera. When seeing problems like this, it’s important to try to decompose the problem into smaller parts. The simple polygon can easily be split into smaller polygons such as triangles, rectangles, trapezoids, etc. But there is one shape to which every simple polygon can be reduced. That shape is the triangle. Every simple polygon can be triangulated, and in any triangulation of a simple polygon, there will be n-2 triangles, where n is the number of vertices in the polygon.
The Art Gallery Theorem:
To cover every part of the simple polygon with n verticies, it will take n/3 truncated (rounded down) cameras at most. The scenario given by Chvátal was the following:
The simple polygon on the right has a total of 14.14 / 3 truncated, which is 4 cameras, which does match the optimal answer for this given polygon. In this given polygon, no camera can possibly ever cover two of the spikes. Forcing the number of cameras to be equal to the number of spikes
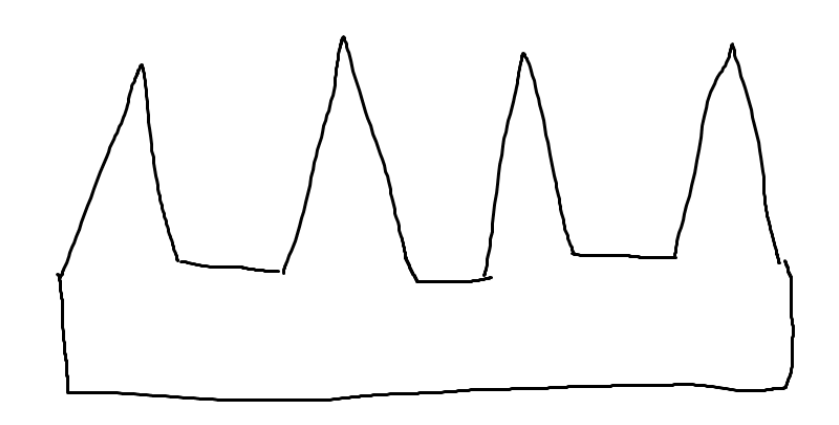
Getting an Answer from a Triangulation:
Let’s say the polygon was already triangulated. How would the optimal answer be found given this triangulation? How the triangulation will be found will be mentioned later. The 3-color vertices of the polygon will be found. A coloring of the graph is where every node on a graph is given a color, and adjacent nodes must never share the same color. A three-color scheme implies that only three colors are being used at most. The vertices of our simple polygon are guaranteed to be able to be colored in only three colors. The vertices represent an outerplanar graph, which is a graph where every node is also on the outside of the graph and no edges cross.
To construct this process of coloring the dual of a graph, The dual of the graph will put a node in each of the “cells” (triangles in this case). There exists an edge between two nodes in the dual graph if two cells share at most one edge with each other. The algorithm starts by selecting a leaf node in a dual graph (a node with no children). The algorithm will then assign three colors to the three different vertices of the starting triangle. Then, the algorithm will travel to other nodes using the dual graph, making sure not to revisit a node. With this current method, at every new triangle, only one vertice will be shared with the previous triangle. This means the problem is as simple as selecting the color that isn’t one of the two already existing vertices.
After coloring the entire graph, Selecting all of the color vertices to place cameras on will produce decently optimal answers. The number of each colored veritice isn’t split evenly all of the time. So, the best answer lies in the color that has the fewest verticies of that color.
Getting a Triangulation, Part 1:
For getting a triangulation, it would be ideal if the simple polygon could be broken up into different convex polygons, but that is a little too hard. A y-monotone polygon will have to do. A y-monotone polygon is a polygon where no horizonal line will break the shape into three or more different groups. Triangulating a simple polygon will start by identifying certain different types of scenarios.
For triangulating multiple different y-monotones, shapes need to be found. If there are any split or merge vertices, then a y-montone shape is not possible. Since each of the scenarios alone will break the y-monotone polygon property, The start and end vertices will be fine. A simple polygon can’t be y-monotone as long as there are split or merged vertices, so they will have to be removed using diagonals. When adding a diagonal to fix the vertex, the diagonals have to obey two rules. The two diagonals must not cross with another diagonal, and they must not cut the borders of the simple polygon.
Dealing with Split Verticies:
Whenever a split vertice is found, there is a left and right edge neighbor. If a horizontal line is drawn on top of the vertex, the first edge that touches on each side are the left and right vertices. Multiple vertices will share the same left-neighboring edge. The split vertex should be connected to a node that has the lowest y-value and shares the same left valve. By choosing the lowest y-value, it guarantees that the area between the two left-pointing lines has no vertices. If there was a node in that area, the current candiadate node wouldn’t have been the one being considered. It is also impossible for a diagonal to insert through the line made between the split vertex and the other end point of the vertices. That endpoint was chosen because it shared the same neighbor. If a line cut through that diagonal, the two would have never been considered as they don’t share the same neighbors.
Dealing with Merge Vertices:
Solving for merge vertices is also simple once the solution for split vertices is done. Merge vertices are more or less just upside-down split vertices. So, if the simple polygon was flipped on its x-axis, then all of the merge vertices could just be calculated using the previous algorithm used for getting split vertices. There need to be a few modifications due to the location of the merge vertices. When the sweep line is going through the vertices, when an “upside down merge vertice” is found, it becomes the diagonal with the current left neighbor. Once the sweep line finds another vertice with the same left neighbor, it will be connected to the candiadte.
However, it might be the case where a merge vertex becomes the candidate node but doesn’t find another node to connect. In that case, make sure to assign it to the last node that shares the same left neighbor before it is removed. The current merge node might also be a helper node for another merge node. In that case, the other middle vertice will be treated in the exact same way.
The final time complexity of the algorithm to split a simple polygon into multiple different y-monotone polygons works in O(n log n).
Getting a Triangulation Part 2:
Now, that a bunch of y-monotone polygons have been created from the initial polygon how can they be turned into the triangulation. A y-monotone polygon can be turned into a triangulation in O(n) time. The algorithim is a simple greedy solution which goes from to to bottom. Going from top of bottom fo the y-monotone polygon a once there are three nodes the current node wil check to see how many nodes it can connect to. It will connect to as many as possible and the process will continue. The following algorithim is implemented using a stack. There are two different scenarios which can be proven to be the only ones that exist.
First Scenario: The node that is currently being explored is on the opposite side of the top of the stack. In this case, the stack will be popped, and an edge will be created between the current node and every other node in the stack.
Second Scenario: The node of the stack is on the same side as the node that is currently. The stack will continued to be popped but, instead of adding an edge instantly whether the two points see each other has to be determined aswell.