Linear Transformation
Linear transformations describe an input vector being moved over to another output vector.
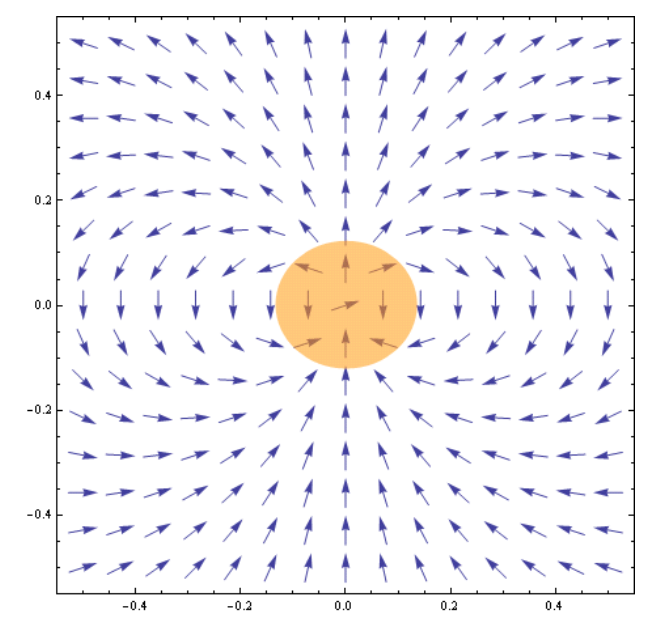
For visualization purposes, it is important to understand what a vector field is. A vector field is generated by passing a vector into a function that spits out another vector. A vector function has some type of transformation within the instruction, and the vector field is every single output vector. Since it is very difficult to see anything when all vector values are shown, most of the time, vector field visualizations don’t show all of them. One of the most famous vector fields is the one that describes magnetism.
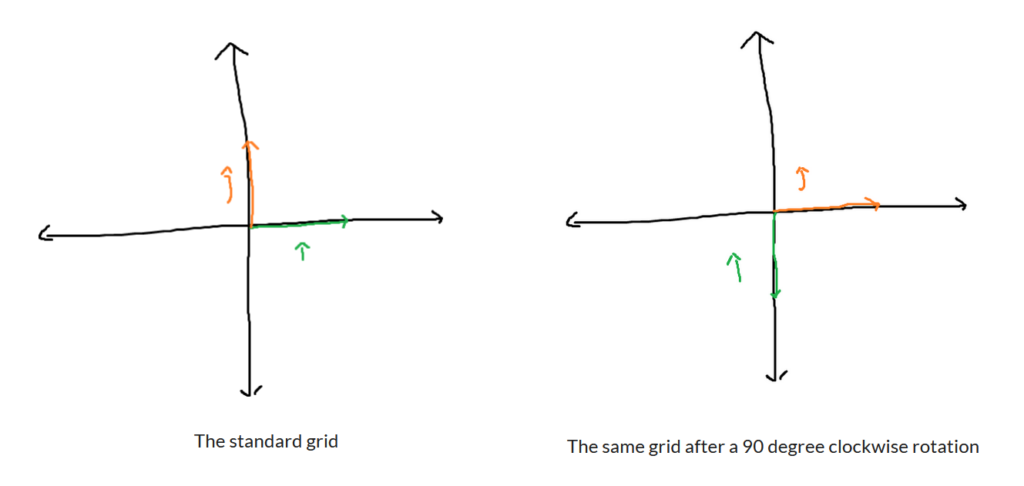
You can imagine that when a transformation is applied to every single vector, it’s fair game to also shift the grid lines around as well. Use the location of i and j as a reference. Here is a 90-degree rotation clockwise.
The transformation can be more complicated, and grid lines can even become diagonal. Below is an example of a shear transformation. Taking the blue image to the green image You can see that the grid lines are no longer straight.

The magnetism vector field does describe a transformation upon a vector. However, it is a not a linear transformation. A linea r transformation requires that the grid lines remain parrellel to each other and that they are spaced evenly. Keeping transformation linear brings about an important property. Remember that any vector can be described as some sort of combination between the unit vectors. Observe the following
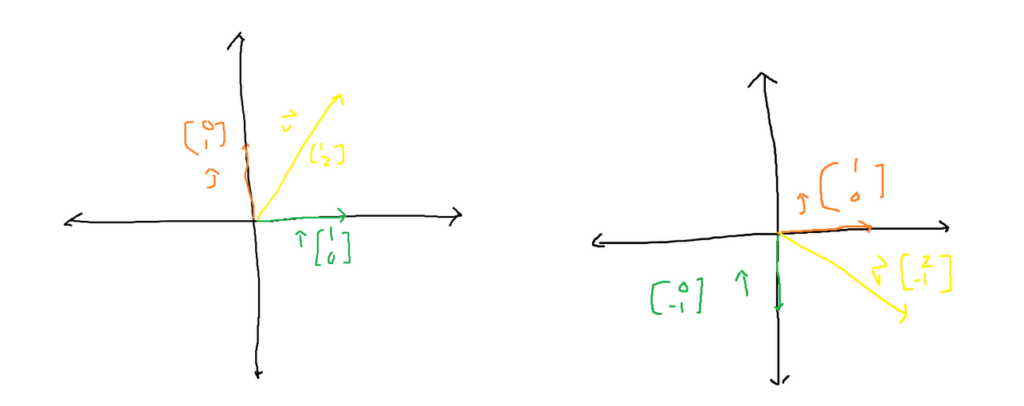
During the transformation, the unit vectors were moved around as well as the rest of the vectors, like vector v. Vector v is a combination of both unit vectors. After the unit vectors are transformed, the transformed vector v still keeps the exact same combination, but this time with the altered unit vectors. This means that to describe a transformation in two dimensions, only two unit vectors are needed. Since everything else will change in accordance with how the unit vectors will change, Given a vector, if the unit vectors after the transformation are given, the vector can be computed by doing the following since every vector is a combination of the unit vectors.
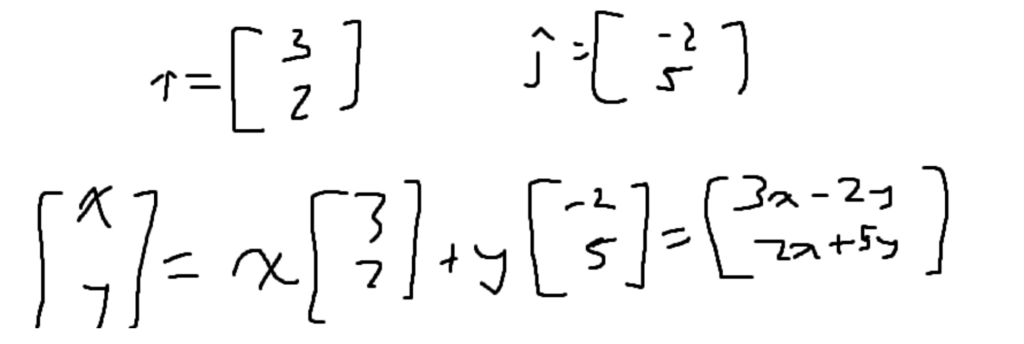
Most of the time, these two unit vectors are stuffed into an n*n matrix, where n is the number of dimensions. The following matrix is called a transformation matrix.
A linear transformation of a vector can be described using the following generic formula: This is an example of vector matrix multiplication.
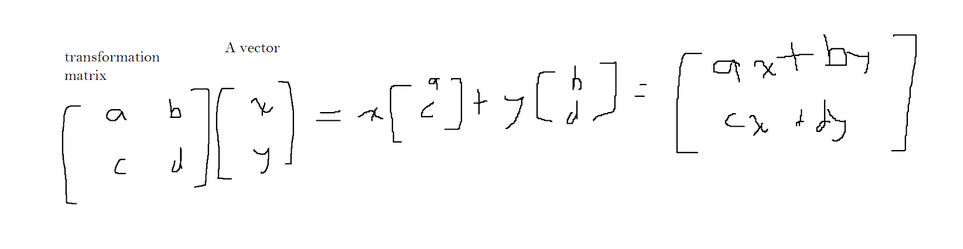
Cross Products:
A cross product between two vectors will yield another vector, unlike the dot product, which gives a scalar value. When adding two vectors A and B, there are two ways to get the final vector. Vector A can be added to B, or Vector B can be added to A. If the vector addition of both ways is displayed at the same time, they form a paralleogram.
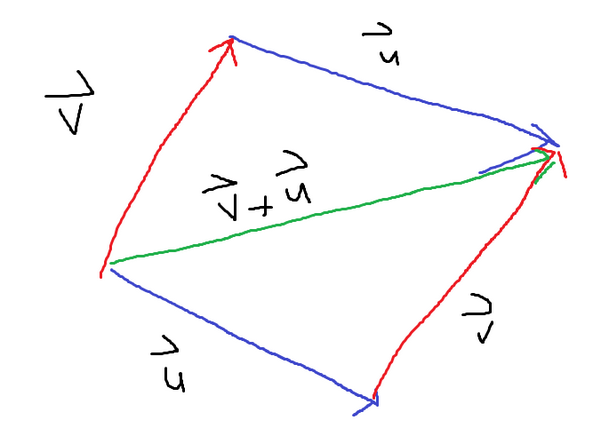
To get the resultant vector for taking the cross product of two vectors, use the area of the paralleogram. The magnitude of the resultant vector will be equal to the area of the parrelogram. Finding the area of the parallelogram is equivalent to determining both of the vectors. The determiner says how the area enclosed by the unit vectors changes after a linear transformation. The two vectors in the cross product are all just linear transformations on the two unit vectors. If the two unit vectors are [1, 0] and [0, 1], they have a total enclosed area of 1 unit. If the determiner is 9, then it is saying that the shape is 9 times bigger than the original area of 1. Which is why the determinant of the two vectors is equivalent to the area of the parrelogram. Because the determiner is being used, it is also possible to have negative values at this point in time.
We have one portion of what we need to fully describe the vector, which is the magnitude. Remember, the magnitude is equivalent to the area of the parrelogram, which is also the determiner. The resultant vector will always be perpendicular to the parrelogram that is formed. However, there are two different perpendicular lines. The correct perpendicular line can be determined with the right hand. Using your pointer and middle finger, attempt to mimic the location and direction of each of the two starting vectors. Next, point your thumb up. The direction of your thumb is the direction of the resultant vector.
Change of Basis:
We all know that a vector is some combination of the two basis vectors or unit vectors. We know that these unit vectors aren’t always the same as they can undergo linear transformations. If two people are using different basis vectors, then a vector describing the scaling of each vector based on those two different unit vectors makes no sense. In the following example, both images show a vector with an x component of 1 and a y component of y. But because in the second image, the definitions of [1, 0] and [0, 1] are different, if one vector is translated to the other basis vectors, they won’t be the same vector. It’s like the two images are speaking two different languages, and they need to be translated beforehand.

The only value that the two images can agree on is the value of the origin. Since, no matter the unit vectors, the absence of both results in a [0,0] vector, The direction of the axis and grid lines can be completely different. If we know the coordinates of her unit vectors in our vector space, then we are able to translate between the two. If we know that in their language the equivalent vectors to their unit vectors are [1, 1] and [1, 1], then we can translate their interpretation to ours. Let’s say that vector v is [1, 1] in their vector space. By some matrix vector (where the matrix is their unit vectors translated to our language) multiplication, we can figure out that [1, 1] in their language actually means [2, 0] in our space. The matrix that is multiplied by their vector to translate it is called the “Change the Basis Matrix.”.
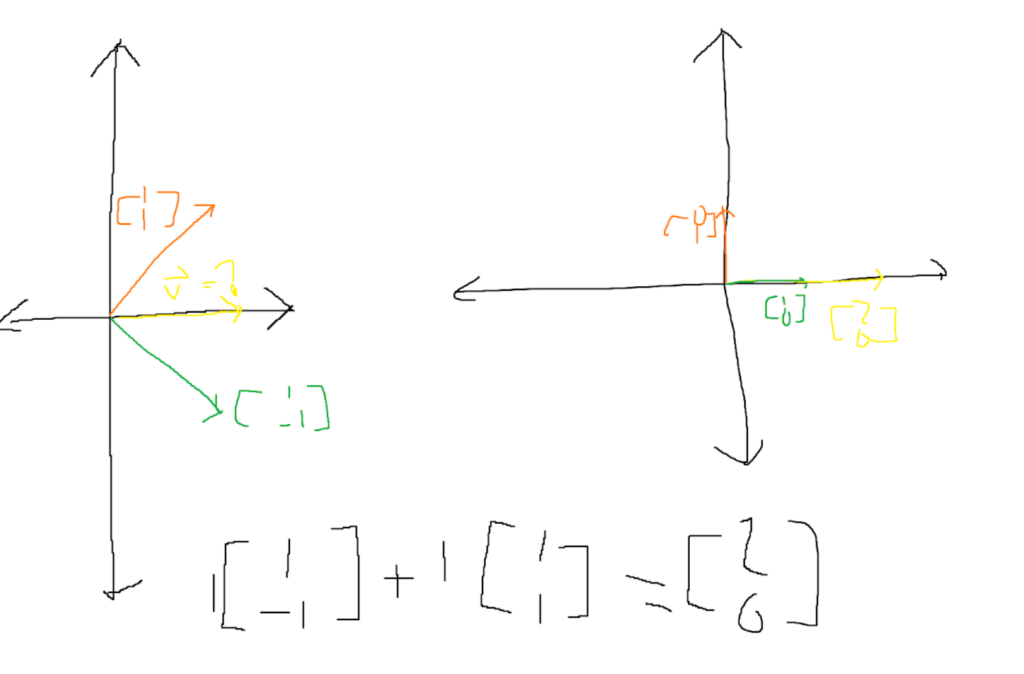
We now know how to translate vectors between languages. But how about doing this with a transformation? To formulate this process, it’s important to understand how to take the inverse of a matrix. Remember, the inverse of a matrix is the matrix that, when multiplied, will yield the identity matrix. The identity matrix is the matrix that has 1’s across the main diagonal (top left to bottom right) and 0’s everywhere else. It’s the equivalent of doing nothing to the unit vectors, which is why it’s called the identity matrix. Translating a vector from one vector space to another goes as follows: Remember that this is matrix multiplication, which multiplies from right to left.
[inverse of changing the basis matrix] * [transformation] * [change the basis matrix] * [vector in a different vector space]
First, we take the vector; then, we change the basis vector to our basis vectors. Then, we apply the transformation to our vector space. If needed, we translate that new vector back into the vector’s original vector space.