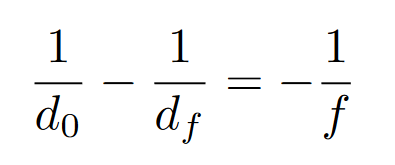Many of us already know that when you shine a light at water, some of the light will be reflected. It’s important to note that the order of “individual light rays” before and after they hit the water is reversed. The reversing of the light rays is what causes our own images in the water to also be shown in reverse.
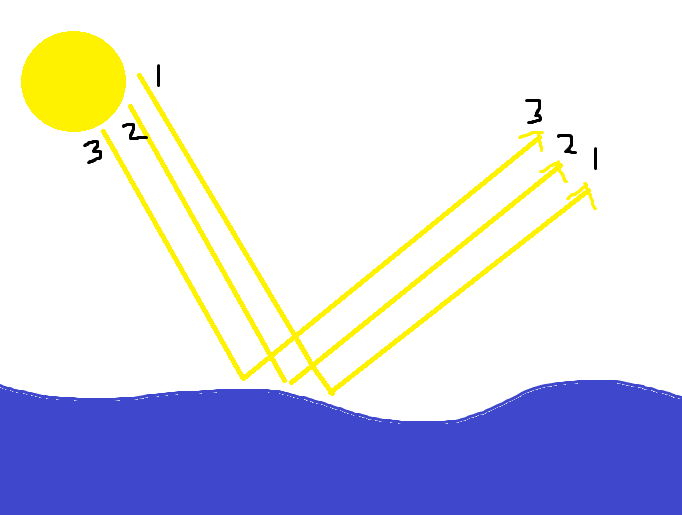
The reflected ray of light will also leave the surface at the same angle that it came in at. The angle is measured not from the surface but from the vertical. The angle at which light comes from is better known as the angle of incidence.
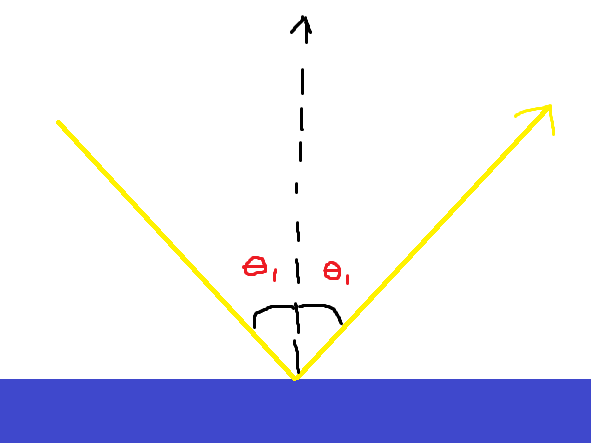
Some of the light is reflected, but some of the light is also refracted. Refraction occurs when light bends after entering a different medium. A change in medium might be along the lines of light transitioning from moving in air to moving in water. Refraction is the reason why some things look weird when placed in water. Light is bent, and therefore the image we receive back is also bent.
We define the angle of refraction as the new angle that is formed with the light ray after entering the medium and the vertical. Below is an image of light traveling through two different mediums. The angle of incidence is theta 1, and the angle of refraction is theta 2.
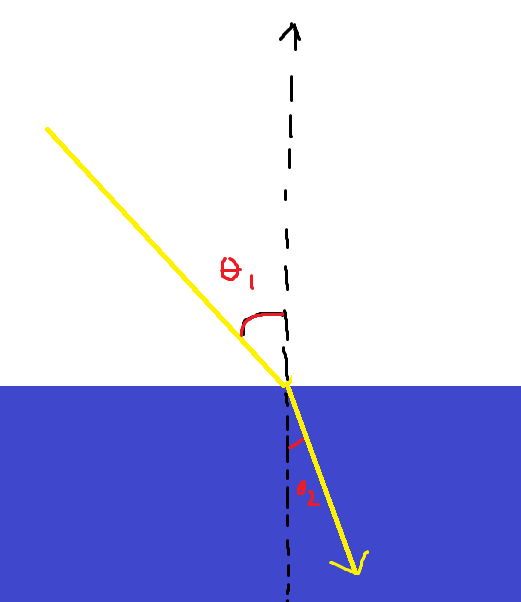
Snell’s Law
Snell’s law describes the relationship between the mediums, the angle of incidence, and the angle of refraction. In Snell’s law, he employs the definition of the index of refraction. Every medium has a different index of refraction. The index of refraction (n) is a constant and is the ratio between the speed of light in a vacuum and the speed of light in that medium. Mediums will slow down the speed of light due to the interaction between the light and the particles. With that out of the way, Snell’s law is as follows:
For reference, the index of refraction for air is basically one, and the index of refraction for water is roughly 1.33. There are a bunch of different things that could affect the refractive index, such as temperature, but I don’t know anything about that.
Below are examples of what low amounts of refraction and high amounts of refraction look like:
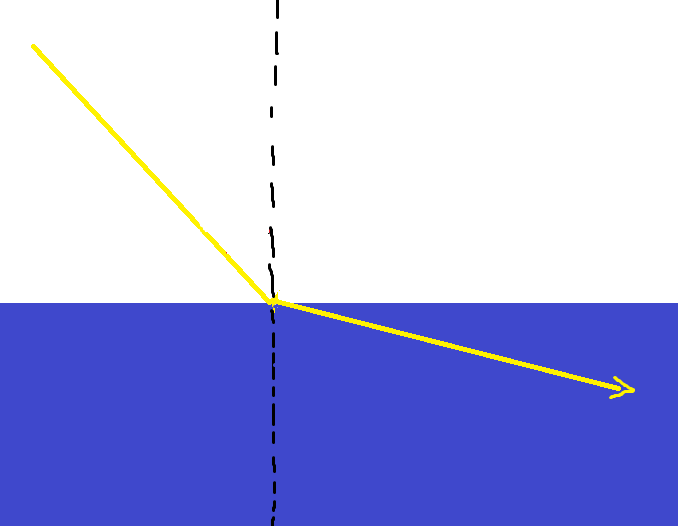
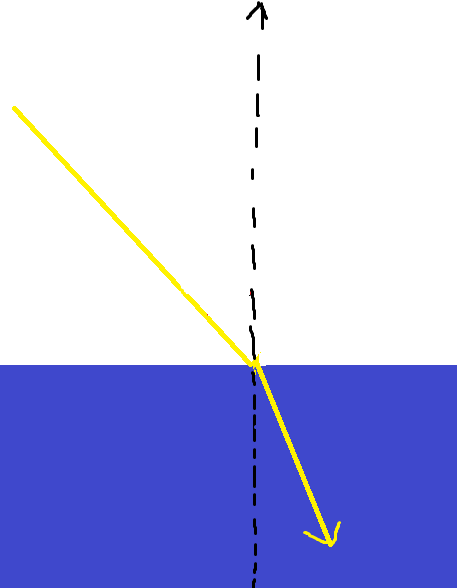
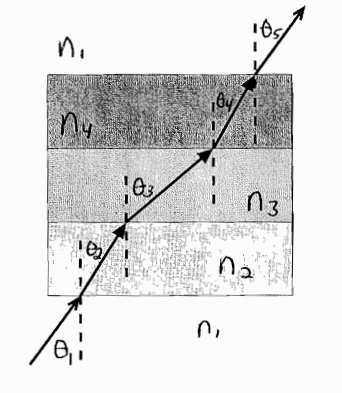
It is obviously possible for light to pass through multiple different mediums. In that case, light can be refracted multiple times.
Lenses and Images
We consider an image to be a real image if the rays from an object cover some location, such as your eye or some other surface. A real image occurs when the light rays actually meet.
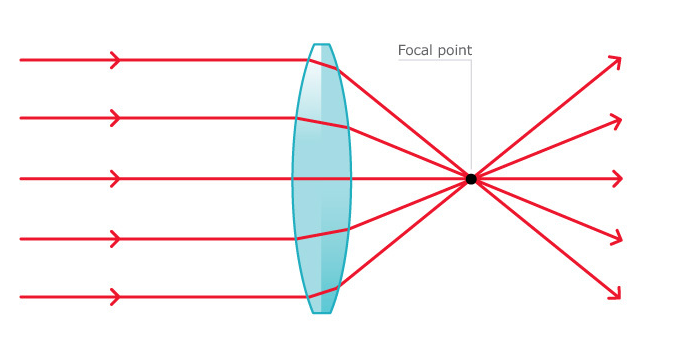
A normal mirror will produce a virtual image. It’s called virtual because it displays what isn’t actually real (the light rays do not actually meet at a specific point). When you look at yourself in the mirror, you are seeing a reversed image of yourself (your mirror image). while a convex lens will focus light, creating a real image. An example of a convex lens is a magnifying glass. The middle of the lens converges on the center and enlarges whatever is there.
The focal length is defined to be equal to the radius of the lens curvature divided by two. By using the focal length we can define two different focal points: one in front of the lens and one behind the lens.
The power of a lens is then defined as the following:
Convex Lens
Lenses that cause light to converge to one point are called “converging lenses”. You will be able to see a real image of objects if they appear after the farther focal point.
.PNG&f=1&nofb=1&ipt=fae7537169c070bab4a96a5cfd88a904f5fded925f967dc20eda50bcd0579076&ipo=images){kind=link}
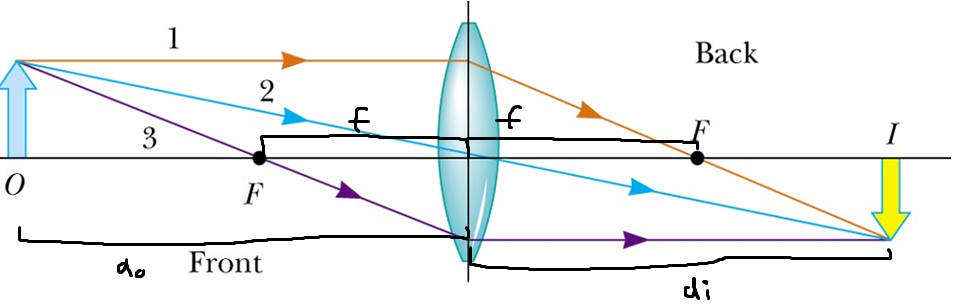
In the above example, the convex lens will produce an upside image because the light rays converge under the principle axis. It turns out that convex lenses will always create upside-down, real images. The image produced by the lens is also smaller than the actual object.
If you want to learn how to figure all of this out on your own, refer to a video like the following (I do not own the video that is listed):
https://www.youtube.com/watch?v=vkNF8tb3Guc
The video includes methods for both convex mirrors (what was just talked about) and concave mirrors (also referred to as diverging lenses).
For a convex lens, the distance of the object, image distance, and focal lengths are all connected through a single equation.
Diverging Lens
Diverging lenses share similar properties, like focal length; however, these lenses cause the light rays to never converge (hence the name diverging lens). Despite the fact that the light doesn’t converge, we still see an image. The light effectively “virtually” converges in order to produce a virtual image.
The virtual light rays converge before ever reaching the mirrors. Producing an upfront image. In our scenario, the images also appear smaller than the actual object. Again, if you want to learn how to figure this out on your own, refer to the video above (which I do not own).
The properties of a diverging lens and its images can also be linked through the exact same equation as those of a convex lens. One caveat is that the focal length for a diverging lens (since the image appears before the lens) is negative, so the equation is more akin to the following:
