Introduction:
Hamiltonian mechanics is yet another way to describe the world around us. Lagrangian mechanics is built upon Newtonian mechanics, and Hamiltonian mechanics does the same for Lagrangian mechanics. The usefulness of the Hamiltonian exists mostly abstractly, as there are very few classical mechanics problems that are easier to solve with Hamiltonian mechanics than the lagrangian. In Hamiltonian mechanics, values are expressed as generalized coordinates and momentums. I do not trust myself to explain how you get from the lagrangian to the Hamiltonian, so here is a link. Also, Wikipedia is good, although it is really math-heavy. The hamiltonian can be expressed as the sum of all generalized momentum times the rate of some coordinate minus the lagrangian.
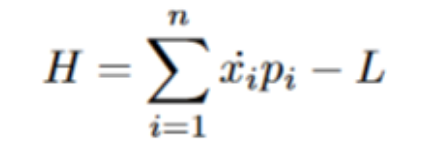
If you want a relation to the physical world instead of just generalized coordinates, here is the following proof for why the Hamiltonian is equal to the total energy (H = KE + PE). This will be important for later.
As mentioned before, the Hamiltonian isn’t ideal for classical mechanics. It shines the most in quantum physics and more modern applications (which I have no clue about; hence, I’m not going to talk about them). However, I decided to give an example of solving for the equation of motion of a spring system using the Hamiltonian anyway. While solving using the Hamiltonian, the goal is to first convert velocities into momentums. Then, differentiate with respect to each independent variable and plug into a modified lagrangian that minimizes the function, guaranteeing the least action. If you just started with lagrangian, you could have avoided the whole conversion into momentum, which is why lagrangian is almost always easier.

Hamiltonian Mechanics and Noether’s Theorem:
Noether’s Theorem states that conservation laws exist if and only if symmetries exist. Noether was able to mathematically prove conservation laws. Up to this point, we assumed that energy was conserved because we observed that energy didn’t change in a closed system. That observation turned out to be wrong, but it was really all speculation at the time. In her paper, she explicitly proved conservation of linear momentum, angular momentum, and energy. However, she also provided a method for deriving any conservation law from any sort of transformation. By mathematical means, symmetry occurs when an object undergoes some transformation and you can’t tell the difference between the objects after the process.

The transformation could be anything, but Noether described translational, rotational, and time symmetry. In translational symmetry, the total energy makeup doesn’t change in accordance with the location of each object. An example of this might be moving a single particle system to the right. The system is exactly the same whether the particle stayed in the same spot or was moved up, down, left, or right. There are no external forces on the particle that depend on distance.
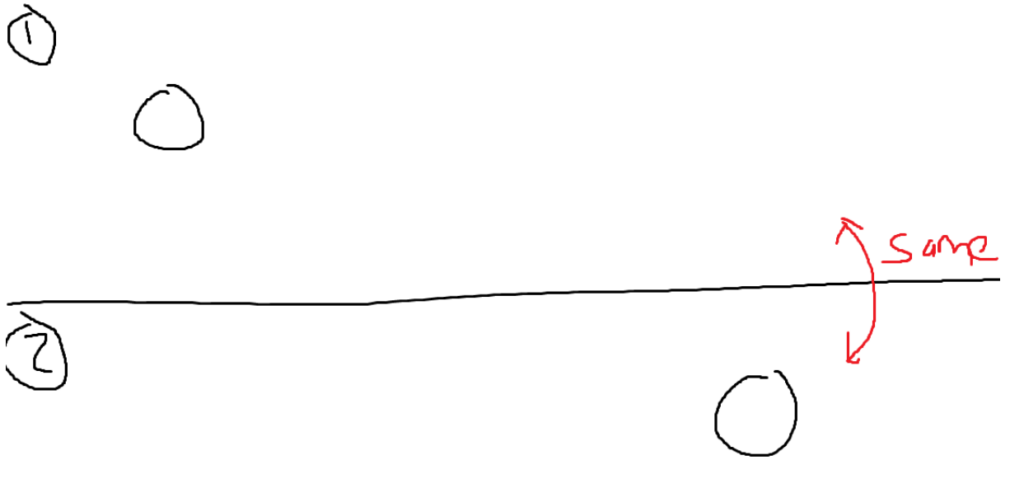
By the same definition, the real number line is also translationally symmetrical because the distance between each number remains the same. The number line is the same whether all the numbers are shifted +5, -3, or not at all.
However, let’s add something to the single particle example that would make it not translationally symmetrical. Assume there is a giant mass (the green part) that exerts a gravitational force on the particles. Now the second particle will experience much more pull from the object because it’s closer. That makes the system not translationally symmetrical anymore because total energy is a function of distance from the green mass.

Rotational symmetry occurs when objects are orbiting. If you assume that the moon travels in a circle around the Earth, then moving the moon forward 90 degrees doesn’t change the force it feels from the Earth because the distance remains the same. However, in reality, the moon orbits the Earth in an ellipse. If you push the moon 90 degrees forward in its orbit, it will be either closer or farther away from the Earth, changing the total energy of the system.
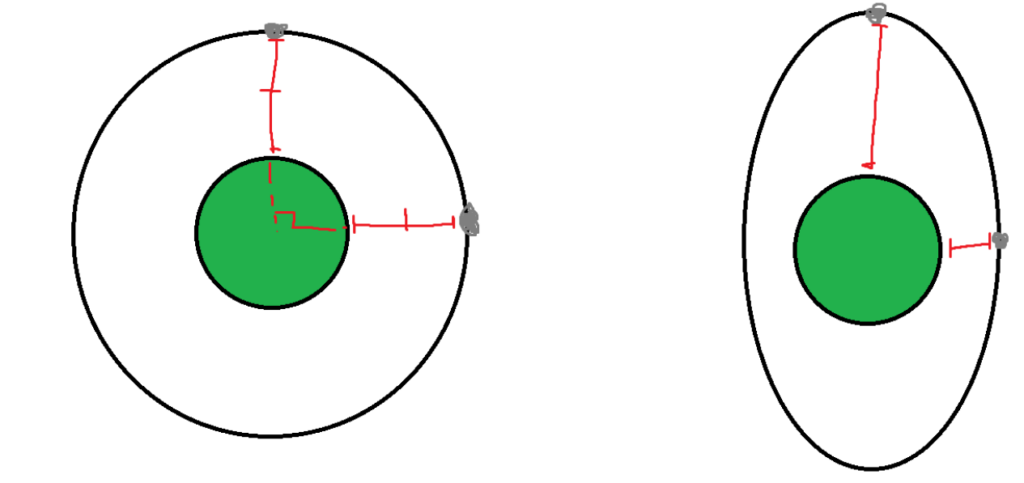
If, after any amount of time, the system remains the same, it has time symmetry. Multiple examples already have time symmetry. In the circular orbit example, no matter how long you wait, the system will always remain the same. That is also true in the example with a singular particle with no interference. In the example where there is a green object and a particle moving towards it, it does not have symmetry. The object will accelerate towards the green mass, and the system will look radically different depending on its time.
In Noether’s paper, she stated that momentum is conserved if and only if there is translational symmetry, that angular momentum is conserved if and only if there is rotational symmetry, and that energy is conserved if and only if the system is time translational symmetric. This means that in the single particle system, momentum, angular momentum (since rotating around any point is equivalent to just translating), and energy are conserved.
Noether used Hamiltonian mechanics in order to prove her theorems. Below is the proof that a system that is time-translational symmetric will conserve energy.
As per definition, the lagrangian and hamiltonian for a typical spring system are:
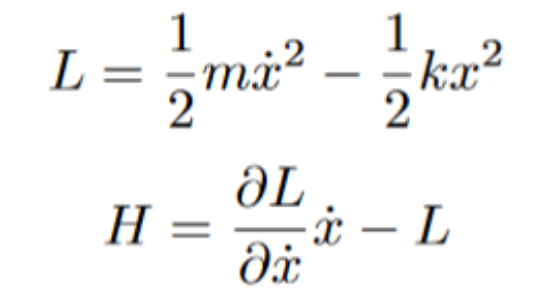
What we want to do is check if the Hamiltonian is conserved under time translation. To check, we want to differentiate the Hamiltonian with respect to time to see how it changes.
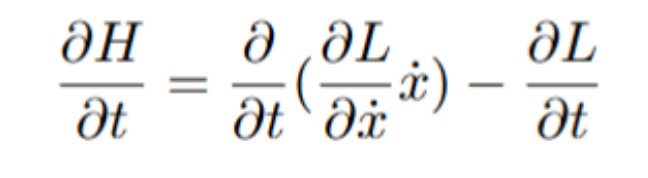
Use the chain rule to differentiate the first term. Use the total derivative in order to differentiate the lagrangian with respect to time (second term).
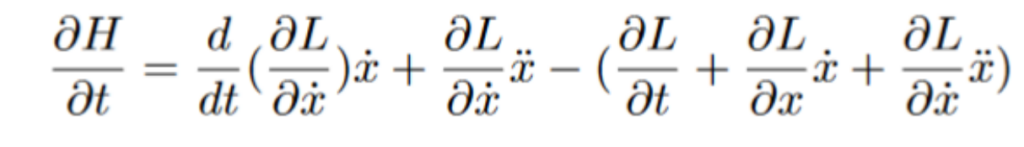
Simplifying the terms:
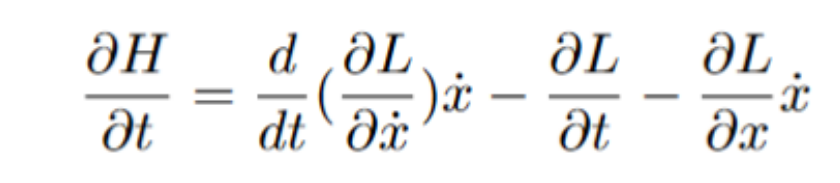
Factoring the x dot:
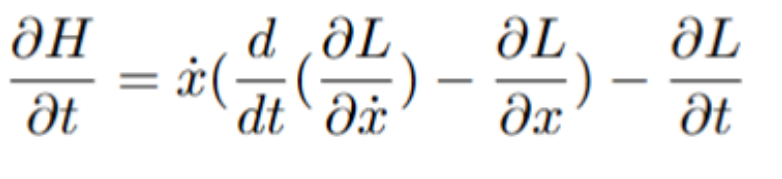
It turns out that the value inside the parentheses is actually something we already know. It’s the Euler-Lagrange differential equation, which we know to be equal to 0. This leaves us with only the following:
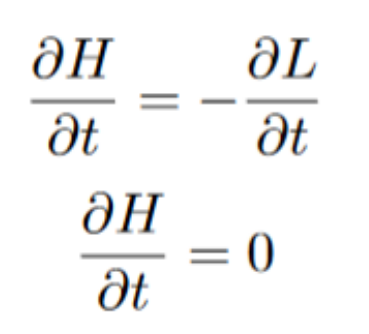
Since the lagrangian doesn’t explicitly vary at all with respect to time, the partial derivative is equal to zero. This leaves us with the change in the Hamiltonian with respect to time being zero. We know that the Hamiltonian is equal to the total energy, so the total energy doesn’t change, meaning it’s conserved.